CS 377P: Programming for Performance

Assignment 5: Shared-memory parallel programming

Due date: April 17th, 2018, 11:59 PM

You can work independently or in groups of two.
Late submission policy: Submission can be at the most 1 day late with 10% penalty.

This assignment has two parts. In the first part, you will implement parallel programs to compute an approximation to pi using the numerical integration program discussed in class. You will implement several variations of this program to understand factors that affect performance in shared-memory programs. In the second part of the assignment, you will implement a parallel program to implement the Bellman-Ford algorithm for single-source shortest-path computation. You may use classes from the C++ STL and boost libraries if you wish. Read the entire assignment before starting work since you will be incrementally changing your code in each section of the assignment, and it will be useful to see the overall structure of what you are being asked to do.

Numerical integration to compute an estimate for pi:

A sequential program for performing the numerical integration is available here. It is an adaptation of the code I showed you in class. The code includes some header files that you will need in the rest of the assignment. Read this code and run it. It prints the estimate for pi and the running time in nanoseconds.

What to turn in:

Use your knowledge of basic calculus to explain briefly why this code provides an estimate for pi.

In this part of the assignment, you will learn the use of atomic updates. Modify the sequential code as follows to compute the estimate for pi in parallel using pthreads. Your code should create some number of threads and divide the responsibility for performing the numerical integration between these threads. You can use the round-robin assignments of points in the code I showed you in class. Whenever a thread computes a value, it should add it directly to the global variable pi without any synchronization.

What to turn in:

Find the running times (of only computing pi) for one, two, four and eight threads and plot the running times and speedups you observe. What value is computed by your code when it is run on 8 threads? Why would you expect that this value is not an accurate estimate of pi?

In this part of the assignment, you will study the effect of true-sharing on performance. Modify the code in the previous part by using a pthread mutex to ensure that pi is updated atomically.

What to turn in:

Find the running times (of only computing pi) for one, two, four and eight threads and plot the running times and speedups you observe. What value of pi is computed by your code when it is run on 8 threads?

You can avoid the mutex in the previous part by using atomic instructions to add contributions from threads to the global variable pi. C++ provides a rich set of atomic instructions for this purpose. Here is one way to use them for your numerical integration program. The code below creates an object pi that contains a field of type double on which atomic operations can be performed. This field is initialized to 0, and its value can be read using method load(). The routine add_to_pi atomically adds the value passed to it to this field. You should read the definition of compare_exchange_weak to make sure you understand how it works. The while loop iterates until this operation succeeds. Use this approach to implement the numerical integration routine in a lock-free manner.

What to turn in:

As before, find the running times (of only computing pi) for one, two, four and eight threads and plot the running times and speedups you observe. Do you see any improvements in running times compared to the previous part in which you used mutexes? How about speedups? Explain your answers briefly. What value of pi is computed by your code when it is run on 8 threads?

std::atomic<double> pi{0.0};

void add_to_pi(double bar) {
auto current = pi.load();
while (!pi.compare_exchange_weak(current, current + bar));
}

In this part of the assignment, you will study the effect of false-sharing on performance. Create a global array sum and have each thread t add its contribution directly into sum[t]. At the end, thread 0 can add the values in this array to produce the estimate for pi.

What to turn in:

Find the running times (of only computing pi) for one, two, four and eight threads, and plot the running times and speedups you observe. What value of pi computed by your code when it is run on 8 threads?

In this part of the assignment, you will study the performance benefit of eliminating both true-sharing and false-sharing. Run the code given in class in which each thread has a local variable in which it keeps its running sum, and then writes its final contribution to the sum array. At the end, thread 0 adds up the values in the array to produce the estimate for pi.

What to turn in:

Find the running times (of only computing pi) for one, two, four and eight threads, and plot the running times and speedups you observe. What value of pi is computed by your code when it is run on 8 threads?

Write a short summary of your results in the previous parts, using phrases like "true-sharing" and "false-sharing" in your explanation.

Parallel Bellman-Ford implementation:

Recall that the Bellman-Ford algorithm solves the single-source shortest path problem. It is a topology-driven algorithm, so it makes a number of sweeps over the nodes of the graph, terminating sweeps when node labels do not change in a sweep. In each sweep, it visits all the nodes of the graph, and at each node, it applies a push-style relaxation operator to update the labels of neighboring nodes.

You can use and modify the graph construction code provided in assignment 4 for this assignment.

Implement Bellman-Ford algorithm serially, i.e. without any pthread constructs and atomic variables.

Input graphs: use rmat15, rmat22, roadFLA and roadNY. You can use wget command to copy them to your CS space.
All nodes' distances are initialized to the maximum of integer, i.e. std::numeric_limits<int>::max(). Include <limits> in your code to use this function.
Source nodes (with distance 0): node 1 for rmat graphs, node 140961 for roadNY, and node 316607 for roadFLA. These are the nodes with the highest degree.
The output for the SSSP algorithm should be produced as a text file containing one line for each node, specifying the number of the node and the label of that node. Here is the solution for rmat15 graph. If a node is unreachable from the source node, you should output INF for its distance.
The four input graphs are large, so you should debug your implementation with some small graphs. Here is an example small graph and its solution, starting from node 5.

Parallelize your SSSP code with pthread constructs, atomic variables and CAS operations.

One way to parallelize Bellman-Ford is to create some number of threads (say t), and divide the nodes more or less equally between threads in blocks of (N/t) where N is the number of nodes in the graph. In each sweep, a thread applies the operator to all the nodes assigned to it. You can also assign nodes to threads in a round-robin way. Giving all threads roughly equal numbers of nodes may not give you good load-balance for power-law graphs (why?) but we will live with it. Feel free to invent more load-balanced ways of assigning nodes to threads.
The main concurrency correctness issue you need to worry about is ensuring that updates to node labels are done atomically. The lecture slides show how you can use a CAS operation to accomplish this. Read the C++ documentation to see how to implement this in C++.
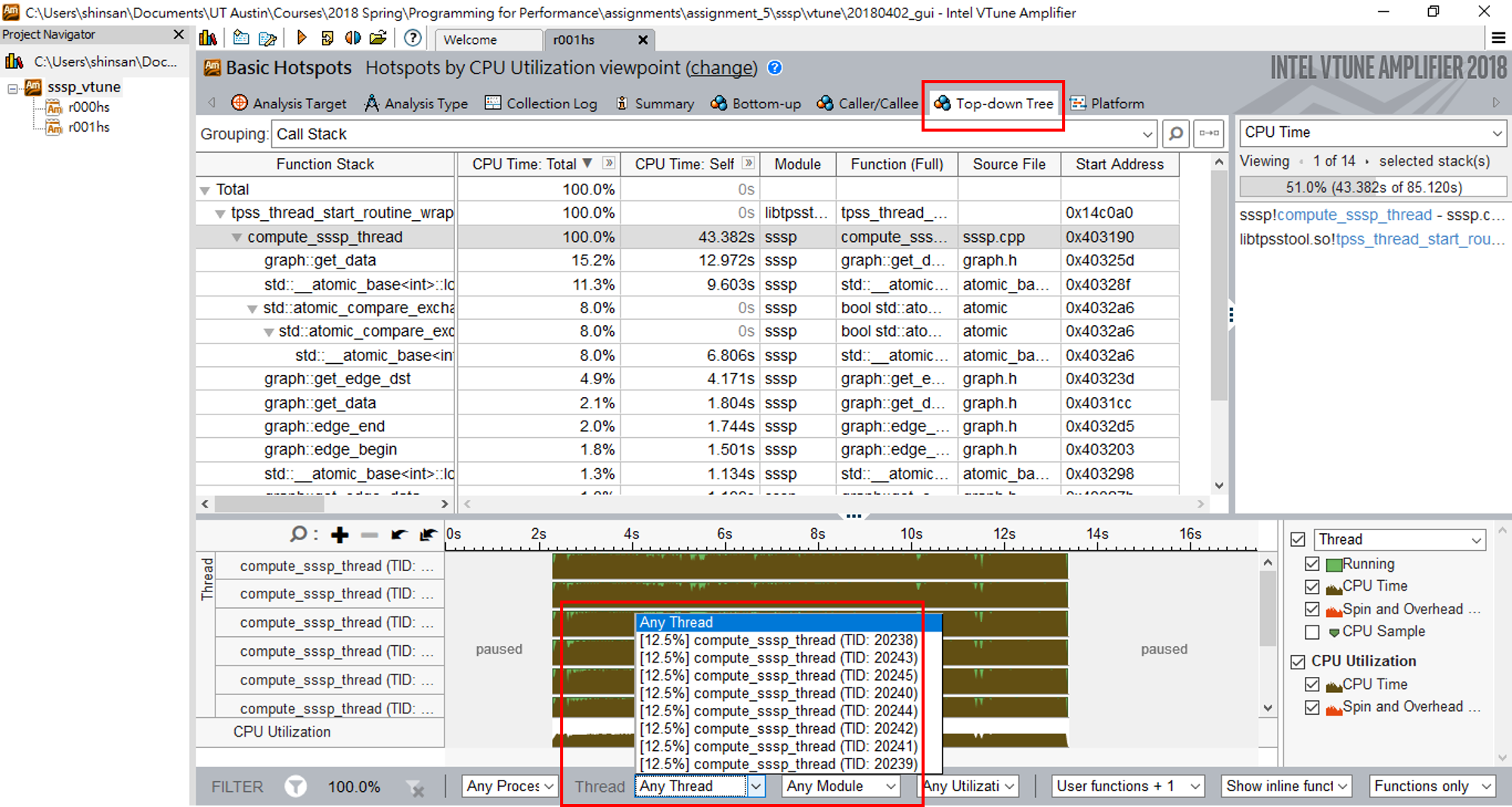
Profile your parallel implementation with 8 threads on roadFLA and rmat22 using the following VTune command:

          amplxe-cl -collect hotspots -analyze-system -start-paused -- <command_line_for_your_SSSP_runs>

Are works balanced among threads? What is the percentage of work being distributed to each thread when running on rmat22? What about that when running on roadFLA?
You can visualize the VTune results to get the information, as shown in the following example:

What to turn in:

Submit the SSSP output produced by your program when it is run on 8 threads for each input graph.
Find the running times and speedups against the serial version for one, two, four and eight threads for each input graph, and plot them. The running time should contain only the main computation for SSSP, i.e. without graph construction, initialization, thread creation/join, and printing results. You can use different plots for the running times for different input graphs since the sizes and therefore the running times will be very different. Use a single plot for the speedups.
Snapshots of VTune hotspots analysis for your SSSP running with 8 threads on rmat22 and roadFLA.
Do you observe good speedups for rmat-style graphs? How about road networks?

Submission

Submit to canvas a .tar.gz file with your code for each subproblem and a report in PDF format. In the report, state both of your teammates clearly, and include all the figures and analysis. Include a Makefile for computing pi and for SSSP, respectively, so that I can compile your codes by make [PARAMETER]. Include a README.txt to explain how to compile your code, how to run your program, and what the outputs will be.

Grading

Numerical integration: 30 points

SSSP: 70 points

Graph formats

Input graphs will be given to you in DIMACS format, which is described below.

DIMACS format numbers nodes from 1, but CSR representation numbers nodes from 0. Hence, node n in DIMACS is node (n-1) in CSR. In other words,

Edge (i, j) from DIMACS should be edge (i-1, j-1) in CSR;
Source node i from command line should be source node (i-1) in your program; and
Report node j in your program as node (j+1) when you do the output.

DIMACS format for graphs

One popular format for representing directed graphs as text files is the DIMACS format (undirected graphs are represented as a directed graph by representing each undirected edge as two directed edges). Files are assumed to be well-formed and internally consistent so it is not necessary to do any error checking. A line in a file must be one of the following.

Comments. Comment lines give human-readable information about the file and are ignored by programs. Comment lines can appear anywhere in the file. Each comment line begins with a lower-case character c.
```
 
c This is an example of a comment line.
```
Problem line. There is one problem line per input file. The problem line must appear before any node or edge descriptor lines. The problem line has the following format.
```
p FORMAT NODES EDGES
```
The lower-case character p signifies that this is the problem line. The FORMAT field should contain a mnemonic for the problem such as SSSP. The NODES field contains an integer value specifying n, the number of nodes in the graph. The EDGES field contains an integer value specifying m, the number of edges in the graph.These two fields tell you how much storage to allocate for the CSR representation of the graph.
Edge Descriptors. There is one edge descriptor line for each edge the graph, each with the following format. Each edge (s,d,w) from node s to node d with weight w appears exactly once in the input file.
```
a s d w
```
The lower-case character "a" signifies that this is an edge descriptor line. The "a" stands for arc, in case you are wondering.

Notes:

When you compute speedup for numerical integration, the numerator should be the running time of the serial code I gave you, and the denominator should be the running time of the parallel code on however many threads you used. The speedup will be different for different numbers of threads. Note that the running time of the serial code will be different from the running time of your parallel code running on one thread because of the overhead of synchronization in the parallel code even when it is running on one thread.