We postulate in [7] that one should never start by considering how to decompose the matrix. Rather, one should start by considering how to decompose the physical problem to be solved. Notice that it is the elements of vectors that are typically associated with data of physical significance and it is therefore their distribution to nodes that is directly related to the distribution of the problem to be solved. A matrix (discretized operator) merely represents the relation between two vectors (discretized spaces): y = A x . Since it is more natural to start with distributing the problem to nodes, we partition x and y , and assign portions of these vectors to nodes. The matrix A should then be distributed to nodes in a fashion consistent with the distribution of the vectors, as we shall show next. We will call a matrix distribution physically based if the layout of the vectors which induce the distribution of A to nodes is consistent with where an application would naturally want them. We will use the abbreviation PBMD for Physically Based Matrix Distribution.
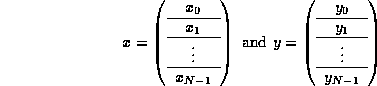
As discussed, we must start by describing the distribution of the vectors, x and y , to nodes, after which we will show how the matrix distribution is induced (derived) by the vector distribution. In the current implementation of PLAPACK, the distribution is derived as follows: partitioning x and y so that
where N >> p . Partitioning A conformally yields the blocked matrix
An explicitly
two-dimensional wrapped distribution for the matrix
can now be obtained by
wrapping the blocks of x and y onto a two-dimensional
mesh of nodes in column-major order,
and assigning blocks of columns 
to the
same column of nodes as sub-vector 
,
and block or rows 
to the same row of
nodes as sub-vector 
. For details, see [7, 9].
We need to clearly state that in the initial implementation of PLAPACK, we only implement this special case. Generalizations are planned.
