Coordinate Systems in Flat

Units

Flat uses the following units for all API-level functions:

   distance:  mm
   angle:     degrees

Coordinate system for a Flat Environment

The Flat environment has a reference frame whose positive X-axis extends to the right, and whose positive Y-axis extends downward. The origin is the upper left corner. Positive angle increases correspond to counter-clockwise rotation, which is contrary to the coordinate system. See here for more details.

The Robot coordinate system

The origin of the robot's coordinate system is the center of the robot (assumed here to be the circular robot "Spot").

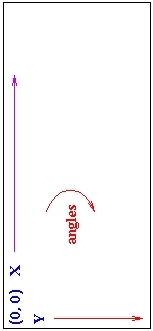
The positive X-axis of the robot extends in whatever direction the robot is facing. Assume this is North. The positive Y-axis of Flat extends East. (In a standard mathematical coordinate system the positive Y-axis would extend West).

This means that angles increase in a clockwise direction, contrary to rotation in a standard Cartesian coordinate frame. So rotating the robot through a positive angle rotates it clockwise.

The Sensor coordinate system

In Flat, the sensors return values based on their own coordinate system, which follows the Spot convention of a positive X-axis straight ahead and positive Y-axis to the right. Distances are FROM THE SENSOR, not from the center of Spot.

For simulated Spot sonars, the sonar-ring radius is 140mm. There are 12 sonars, and sonar 0 faces straight ahead. The sonar numbers increment clockwise (following the Robot coordinate system).

For a one-laser Spot, the laser is mounted on top of the robot (at (0, 0) in Spot-coordinates). It faces forward (0 degrees) and scans a 180-degree interval, from -90 <= theta < 90.

For a two-laser Spot, the lasers are mounted on the sides of the robot at (0, -140mm) and (0, 140mm) for the left and right ones respectively. The lasers are tilted -45 and 45 degrees respectively, again in the Spot coordinate system. (The tilt is outward). Each laser scans 180 degrees, so the sensor readings overlap in front of the robot.

Heads-up Map coordinate system

For display purposes, it is useful to display the output in a "heads-up" display in which Spot always faces North, along the positive Y-axis of a standard standard Cartesian coordinate system.

These values would then have to be converted to the coordinate system of the display window, which typically follows the coordinate system used in the Flat Environment. Usually this involves subtracting the y coordinate from the height of the window.

The process for converting sensor readings to such a display is described below.

Case 1: Readings relative to the robot

Normally, we have the sensor reading r, and its angle relative to the robot in the map coordinate system described above. For the standard 2-laser configuration for Spot, these angles are:

   (225 >= theta >  45)     left sensor
   (135 >= theta > -45)     right sensor

Transforming this to a robot-centric coordinate proceeds as follows:

  Given:
         r      Sensor reading  
         theta  Angle of the sensor reading relative 
                to the robot.
         Xs     X location of sensor on the robot
                in the map coordinate system.
	 Ys     Y location of sensor on the robot
                in the map coordinate system.
         
     The robot-centric coordinates (x, y) are
     calculated as follows, for the angle ranges
     listed above:

       (x, y) <- (Xs, Ys) + polar->rect(r, theta)     (1)
      

  (1)  x' = r * cos(theta),  y' = r * sin(theta)

Case 2: Sensor readings relative to the environment

You may have sensor readings whose angles are relative to the environment's coordinate system. In this case you can convert the coordinates to a "heads-up" coordinate system as follows:

  Given:
         r      Sensor reading  
         theta  Angle of the sensor reading relative 
                to the environment (which depends on the
		orientation of the robot and the sensor angle)
         Xs     X location of sensor in the environment
	 Ys     Y location of sensor in the environment
	 Xr     X location of the robot in the environment
	 Yr     Y location of the robot in the environment
	 Or     Orientation of the robot (angle relative to the
	        environment)
         
     The robot-centric coordinates (x, y) are
     calculated as follows:

       (x, y) <- (Xs, Ys) + polar->rect(r, theta)     (1)
      
     The point is now in environment coordinates.

       (x, y) <- (x, y) + (-Xr, -Yr)        -- relative to robot location
       (x, y) <- rotate((x, y), Or - 360.0) -- undo robot rotation   (2)
       (x, y) <- (-x, y)                    -- convert to normal Cartesian
       

     The following LISP code performs the above operations:

      (setq transformed-point (translate-point (polar-to-rect pt) `(,Xs ,Ys)))
      (setq transformed-point (translate-point transformed-point `(,(- Xr) (- Yr))))
      (setq transformed-point (rotate-point transformed-point (- Or 360.0)))
      (setq transformed-point (reflect-y transformed-point))

  (1)  x' = r * cos(theta),  y' = r * sin(theta)
  (2)  x' = (x * cos(theta) - y * sin(theta))
       y' = (x * sin(theta) + y * cos(theta))

Micheal Hewett
Saturday, 2 October 1999
Last updated: Monday 4 October 1999