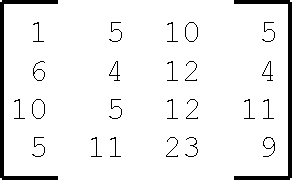
CS 307- Extension Section - Fall 2001
Assignment 4, Matrices
Placed Online: October 8,
2001
Due: Before 11:59:59 p.m. Thursday October 18, 2001
Purpose: To practice programming with 2D Arrays
Provided classes: MatrixGenerator.java
"Linear algebra is a fantastic subject. On the one hand it
is clean and beautiful. If you have three vectors in 12 dimensional space, you
can almost see them."
- Gilbert Strang, Linear Algebra and its applications
Matrices
Background: Mathematical matrices are used to solve systems of linear equations. Matrices are used in applications such as physics, engineering, probability and statistics, economics, biology, and computer science (especially in the area of computer graphics.) The most important case and the simplest is when the number of unknowns equals the number of equations. Matrices appear in the following form:
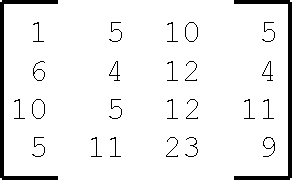
The above matrix has 4 rows and 4 columns, but the number of rows and columns do not have to be equal. Each entry can be an integer or real number. For this assignment you will only deal with matrices of integers. You will implement a class, Matrix, that models a mathematical matrix and supports various operations (behaviors, methods) on matrices. In my explanation of the behaviors you must implement, I will use the following notation for matrices
a1-1 a1-2 a1-3
a2-1 a2-2 a2-3
a3-1 a3-2 a3-3
a1-2 refers to the element in the first row, second column of matrix a.
Requirements: Create a Matrix class. You must use a "native" two dimensional array of ints as your underlying storage container in the matrix class:
private int[][] myMatrix; // or myNums or some other appropriate name
Implement the following methods. Use the method signature listed. Determine the pre and post conditions and list these in comments before each method. If your pre and post conditions are stated clearly you may assume they will be met by anyone using the class. Assume the upper left cell of the matrix is numbered 0,0. Also for each class list the Big O execution time for the method in the comment prior to the method. Assume the method is working on a N by N matrix to determine the Big O execution time. If the Big O execution time is polynomial such as N2 simply use the ^ character: N^2
A default constructor
A constructor that accepts a 2D array of integers and
constructs a matrix with those values.
public Matrix(int[][] mat)
A constructor with parameters for the number of rows, number
of columns, and initial value for all elements:
public Matrix(int numRows, int numCols, int initialVal)
A copy constructor. It shall make a deep copy.
public Matrix(Matrix other)
A method to change the value of a given element in the
Matrix:
public void changeElement(int row, int column, int newValue)
A method to change all the elements of a given row to a
given value.
public void changeRow(int row, int newValue)
A method to change all the elements of a given column to a
given value.
public void changeColumn(int col, int newValue)
Methods that return the number of rows or columns in the
matrix.
public int numRows()
public int numCols()
A Method to change the number of rows or columns in the
matrix. This may be a trimming operation or an expansion. If it is an
expansion make all new values will be 0 or set equal to a parameter for an
overloaded version:
public void changeNumRows(int newNumRows)
public void changeNumRows(int newNumRows, int newValue)
public void changeNumCols(int newNumCols)
public void changeNumCols(int newNumCols, int newValue)
public void changeSize(int newNumRows, int newNumCols)
public void changeSize(int newNumRows, int newNumCols, int newValue)
A method to access a particular value
public int getVal(int row, int col)
A method to add two matrices. Adding matrices is only
possible if they have an equal number of rows and columns.
matrix a
matrix b result of a + b
a1-1 a1-2
b1-1 b1-2 (a1-1 + b1-1) (a1-2 + b1-2)
a2-1 a2-2 b2-1 b2-2 (a2-1 + b2-1) (a2-2 + b2-2)
a3-1
a3-2 b3-1 b3-2 (a3-1 + b3-1)
(a3-2 + b3-2)
Example with values
matrix a matrix
b result a +b
1 5
5 6
6 11
17 3
5 2
22 5
public Matrix add(Matrix rhs)
A method to subtract two matrices. Works almost the same as addition
matrix
a matrix b
result of a - b
a1-1 a1-2
b1-1 b1-2 (a1-1 - b1-1) (a1-2 - b1-2)
a2-1 a2-2 b2-1 b2-2 (a2-1 - b2-1) (a2-2 - b2-2)
a3-1
a3-2 b3-1 b3-2 (a3-1 - b3-1)
(a3-2 - b3-2)
public Matrix subtract(Matrix rhs)
A method to multiply two matrices. This does not work as
you would expect with simply multiplying the matching elements. Instead
matrices may be multiplied as long as the number or columns in the first
matrix equals the number of rows in the second matrix. The resulting has
rows equal to the number of rows in the first matrix and columns equal to
the number of columns in the second matrix. Maybe an example would help?
Matrix a is a N(rows) by M(columns) matrix and matrix b is a K by L matrix.
a * b is allowed if M = K. The result will be a N by L matrix. Here
are the mechanics of matrix multiplication (- removed from notation of
elements):
matrix a(3X2) matrix
b(2X3)
a11 a12
b11 b12 b13
a21 a22 b21 b22 b23
a31 a32
result of a * b
(a11*b11 + a12*b21) (a11*b12 + a12*b22)
(a11*b13 + a12*b23)
(a21*b11 + a22*b21) (a21*b12 + a22*b22) (a21*b13 + a22*b23)
(a31*b11 + a32*b21) (a31*b12 + a32*b22) (a31*b13 + a32*b23)
Example with values
matrix a matrix b
2 4 3 4
1
5 2 1 8
4
result of a * b
(2*3 + 4*1 = 10) (2*4 + 4*8 =
40) (2*1 + 4*4 = 18)
(5*2 + 2*1 = 17) (5*4 + 2*8 =
36) (5*1 + 2*4 = 13)
10 40 18
17 36 13
public Matrix multiply(Matrix rhs)
Create a
method to transpose a matrix. To transpose a matrix the columns are taken
directly from the rows of the original matrix. The ith row of the original
matrix becomes the ith column of the transposed matrix.
matrix a transpose of matrix a
2 4 0 2 5
5 2 12 4
2
0 12
Implement a mutator and an accessor for transposing matrices
public Matrix getTranspose()
public void transpose()
A matrix is symmetric if the transpose of the matrix
equals the original matrix. Write a method to determine this:
public boolean isSymmetric()
An equals method. Note this should be an overriding of the
equals method from Object not an overload
public boolean equals(Object rhs)
A toString method. Allow a total of 6 spaces for
each element with the number left justified in that field. Different rows
shall be on different lines.
public String toString()
The MatrixGenerator class has two methods, getRandomMatrix, and getMatrix.
public int[][] getRandomMatrix(int row, int cols, int
lowerLimit, int upperLimit)
/*generates a row by cols matrix with random values between lowerLimit and
upperLimit inclusive
*/
public int[][] getMatrix()
/*prompts for number of rows and columns from keyboard and then prompts for each
element
*/
You must test the class on your own. Your file will be run against a test file to be graded as well as looked at to ensure you used good style. When you finish turn in your file, Matrix.java, to Mike via email.