For the theorem of Pythagoras, I start from Coxeter's formulation ("Introduction to Geometry", p.8)
"In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the two catheti."
Let us play a little bit with that formulation. In a triangle with sides a, b, and c —different from 0 so as to make its angles well-defined— we introdue the usual nomenclature α, β, and γ for their respective opposite angles. (We introduced one angle name so as to be able to express right-angledness, and the other two for reasons of symmetry.)
A formal expression of Coxeter's formulation is
γ = π/2 ⇒ a2 + b2 = c2 .
Besides the nomenclature we introduced, this formulation contains the (transcendantal!) constant π. Fortunately we can eliminate it thanks to
π = α + β +γ .Elementary arithmetic yields the equivalent formulation
α + β = γ ⇒ a2 + b2 = c2 .Isn't that nicely symmetric? It immediately suggests —at least to me— the strengthening
(This will turn out to be a theorem.) We get an equivalent formulation by negating both sides:
α + β ≠ γ ≡ a2 + b2 ≠ c2 .
But x ≠ y ≡ x < y ∨ x > y , and the latter disjuncts are mutually exclusive. Remembering that the larger angle is opposite to the larger side, is it bold to guess
(1) α + β < γ ≡ a2 + b2 < c2 and(2) α + β > γ ≡ a2 + b2 > c2 ?
Bold perhaps, but not unreasonable.
Note that (0), (1) and (2) are not independent: from any two of them, the third can be derived. They can be jointly formulated in terms of the function sgn —read "signum"— given by
sgn.0 = 0 ∧ (sgn.x =1 ≡ x > 0) ∧ (sgn.x = -1 &equiv x < 0) ,viz. sgn.(α + β - γ) = sgn.(a2 + b2 - c2) .
Consider now the following figure. We have drawn
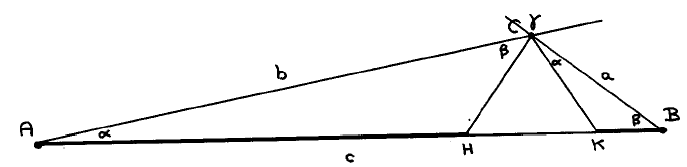
the case α + β < γ, in which the triangles ΔCKB and ΔAHC, of disjoint areas, don't cover the whole of ΔACB; denoting the area of ΔXYZ by "XYZ" we have in this case
CKB + AHC < ACB .
In the case α + β = γ, H and K coincide and we have
CKB + AHC = ACB ,and in the case α + β > γ, the two triangles overlap and we have
CKB + AHC > ACB .In summary
sgn.(α + β - γ) = sgn.(CKB + AHC - ACB) .
The three areas of the right-hand side are those of similar triangles and hence have the same ratios as the squares of corresponding lines, in particular
CKB/a2 = AHC/b2 = ACB/c2 > 0 ;hence
sgn.(CKB + AHC - ACB) = sgn.(a2 + b2 - c2) ,Hence we have proved
sgn.(α + β - γ) = sgn.(a2 + b2 - c2) ,
*
The title of this note could make one wonder why I would waste my time flogging a horse as dead as Pythagoras's Theorem. So let us try to summarize what we could learn from this exercise.
• Three cheers for formalization! Instead of setting out to prove a2 + b2 = c2 for a right-angled triangle, we included the antecedent γ = π/2 in the formal statement of what was to be proved. It was only after the introduction of π that we could eliminate it and met the "nicely symmetric" formulation.• Three cheers for the equivalence! It makes quite clear that the theorem is not about right-angled triangles, but about triangles in general.
• Three cheers for the notational device captured in sgn. If we had not been careful, we would have ended up proving
(α + β) R γ ≡ (a2 + b2) R c2for R any of the six relations =, ≠, <, ≤, >, and ≥
• No cheers at all for that stage of the argument in which lack of axiomatization forced us to resort to a picture. Pictures are almost unavoidably overspecific and therby often force a case analysis upon you. Note that I carefully avoided the pictures for α + β > γ; there are 9 of them: K to the right of A, coincident with A, and to the left of A, and similarly for the pair H and B. For the argument these distinctions are irrelevant but, when drawing a picture, you can hardly avoid making them.
• One of these days I would like to find a convincing explanation of the circumstance that youngsters continue to be educated with the theorem of Pythagoras in its diluted form as quoted from Coxeter. Notice that the 9 figures could have been avoided by also proving
CKB + AHC < ACB ⇒ α + β < γ andi.e. proving (0) and (1) in full.
CKB + AHC = ACB ⇒ &alpha + β = γ ,
• Notice that our figure was not pulled out of a magicians hat! As soon as sgn.(α+β–γ) occurs in the demonstrandum, it is sweetly reasonable to construct that difference. In order not to destroy the symmetry between α and β, one starts with γ and subtracts α at the one side and β at the other:
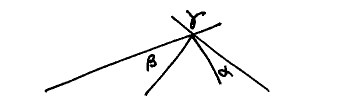
and this is the germ of the figure we drew.
Epilogue. I am in a paradoxical situation. I am convinced that of the people knowing the theorem of Pythagoras, almost no one can read the above without being surprised at least once. Furthermore, I think that all those surprises relevant (because telling about their education in reasoning). Yet I don't know of a single respectable journal in which I could flog this dead horse.
Austin, 7 September 1986
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188, USA
Transcription by Joel Hockey
Last revised on