Problem 10406 from The American Mathematical Monthly, Volume 101, Number 8 / October 1994
10406. Proposed by David C. Fisher, University of Colorado, Denver, CO, Karen L. Collins, Wesleyan University, Middleton, CT, and Lucia B. Krompart, Rochester, MI.
Show that a path on an m by n square grid which starts at the northwest corner, goes through each point exactly once, and ends at the southeast corner divides the grid into two equal halves: (a) those regions opening north or east; and (b) those regions opening south or west.
(10406) A path meeting the conditions of the problem on a 5 by 8 grid is shown in figure 10406 below.

We confine our attention to paths from NW to SE that do not necessarily go through each point; the off-path points are called free. Directing the paths from NW to SE, I identify (here without proof) the region(s) “a” with those to the left of the path, and the regions “b” with those to its right.
A path, along which turns to the left and turns to the right alternate, is a shortest path; we give a simple example (in the same 5 by 8 grid).
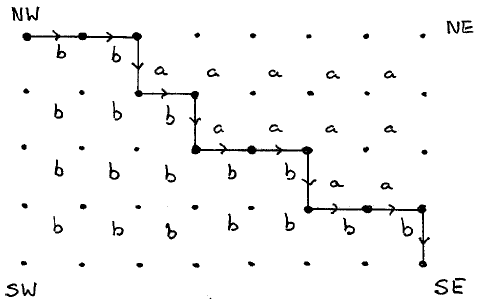
For the m by n grid with a shortest path we observe
• # points = m * n
• # unit squares = (m−1) * (n−1)
• # edges on shortest path = (m−1) + (n−1)
• # points on shortest path = m + n − 1
• # free points = (m*n) − (m+n−1) = (m−1) * (n−1)
in short: the number of unit squares equals the number of free points. But we can go further: this equality holds for the separate regions! We can establish in the a-region a 1-1 correspondence between each unit square and its NE corner, and in the b-region between each unit square and its SW corner.
Introducing
Fa and Fb : # free points in a-region(s) and b-region(s) respectively
Sa and Sb : # unit squares in a-region(s) and b-region(s) respectively,
we can now formulate
Lemma 0 In the case of a shortest path Fa = Sa ∧ Fb = Sb.
The idea of the proof is to start with a given path that visits each point exactly once —i.e., Fa = 0 ∧ Fb = 0—, and to transform it in a finite number of moves into a shortest path for which Fa = Sa ∧ Fb = Sb holds. Initial and final state are then to be linked via an invariant that is maintained by each move.
For the move we consider that, as said, a path, along which turns to the left and turns to the right alternate, is a shortest path. Consequently, if the path is not of minimal length, it contains at least one pair of successive turns in the same direction. With those turns k edges apart it means that there exists a rectangle —a “bar”— of k (k ≥1) unit squares such that 3 of its sides are formed by 1, k, 1 edges of the path, e.g. for k = 5:
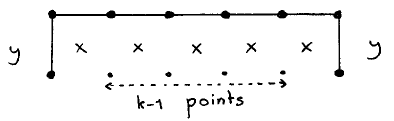
We can —and will— always choose a rectangle such that the k−1 interior points of the 4th side are free. The move shortens the path by 2 edges in the obvious way; in the same example, the above configuration is transformed into
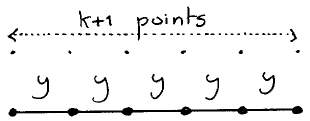
With x,y = a,b or x,y = b,a, we observe for the transformation by the move:
|
∆ Sx = −k ∆ Fx = −(k−1) ∆ (Sx−Fx) = −1 |
∆ Sy = +k ∆ Fy = +k+1 ∆ (Sy−Fy) = −1 |
The above transformation reduces at both sides of the path the difference S−F by 1, and hence
(Sa−Fa) − (Sb−Fb) = q ,
if initially true, is an invariant of our total transformation process (which obviously terminates since each move reduces the path by 2 edges).
From Lemma 0, which is applicable in the final state, we conclude q = 0. Therefore initially, with Fa = 0 ∧ Fb = 0, we have Sa−Sb = 0 or Sa = Sb. Quod erat demonstrandum.
* * *
It took me several hours to design the move of the previous page; for quite a while I considered 2 unparameterized moves: the current one with k =1 and 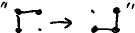 , which changes the shape of the path without shortening it. The mere fact that the second move complicates the termination argument should have made me reject it much faster.
, which changes the shape of the path without shortening it. The mere fact that the second move complicates the termination argument should have made me reject it much faster.
I liked the problem.
Austin, 17 October 1994
prof.dr. Edsger W.Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
USA