We can embed the complete 2-graph with labelled vertices in a 1-dimensional world
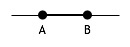 or
or 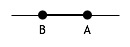
and if the two "ends" of that 1-dimensional world are distinct, the above 2 embeddings are different.
We can embed the complete 3-graph with labelled vertices in a 2-dimensional world
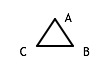 or
or 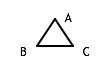
and if the two "sides" of the plane are distinct, so are the 2 embeddings.
Similarly —and this will be our last example— the completed 4-graph can be embedded in 2 ways in directed 3-space —i.e. a 3-dimensional world that is distinct from its mirror image—
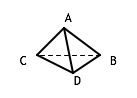 or
or 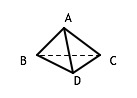 .
.The first question to be raised and answered is: how do we distinguish, for each number of dimensions, between the 2 embeddings? Moreover we would like to do so in a manner that does not destroy the symmetry between the vertices.
Here the theory of inversions —i.e. (the number of) pairs of elements out of order— gives the answer. For any k, k ≥ 2, the k! permutation of k elements can be partitioned into 2 classes of equal size such that a single swap transforms any permutation of the one class into a permutation of the other class. For elements A, B, the classes are {AB} and {BA}, for elements A, B, C, the classes are {ABC, BCA, CAB} and {ACB, BAC, CBA}, for elements A, B, C, D, the one class is {ABCD, ACDB, ADBC, BADC, BCAD, BDCA, CABD, CBDA, CDAB, DACB, DBAC, DCBA} and the construction of the other class is left to the reader. I would like to stress that the existence and "shape" of these classes have nothing to do with the labels A,B,C,… or their alphabetic order: they are intrinsically generated by the process of permuting. The two classes provide the answer to our first question: for any k, we associate the one class with the one embedding, and the other class with the other embedding.
The "oriented" (n+1)-graph has n+1 "faces", one opposite to each vertex. The way to give those faces an orientation in a systematic manner is, for instance, as follows: choose from the representative class for the (n+1)-graph a permutation that starts with the opposite vertex and select the rest of that permutation. So the oriented 3-graph with class {ABC, BCA, CAB} has face BC opposite to A, face CA opposite to B and face AB opposite to C; the 4-graph corresponding to ABCD has the 4 oriented faces corresponding to BCD, ADC, ABD, and ACB respectively, and any 2 of them contain the subface they share in opposite orientation: e.g. BCD and ADC contain CD and DC respectively, the one having been obtained by truncating a leading AB (from ABCD, as a matter of fact), the other by truncating a leading BA (from BADC). Generalization to more dimensions is left to the reader.