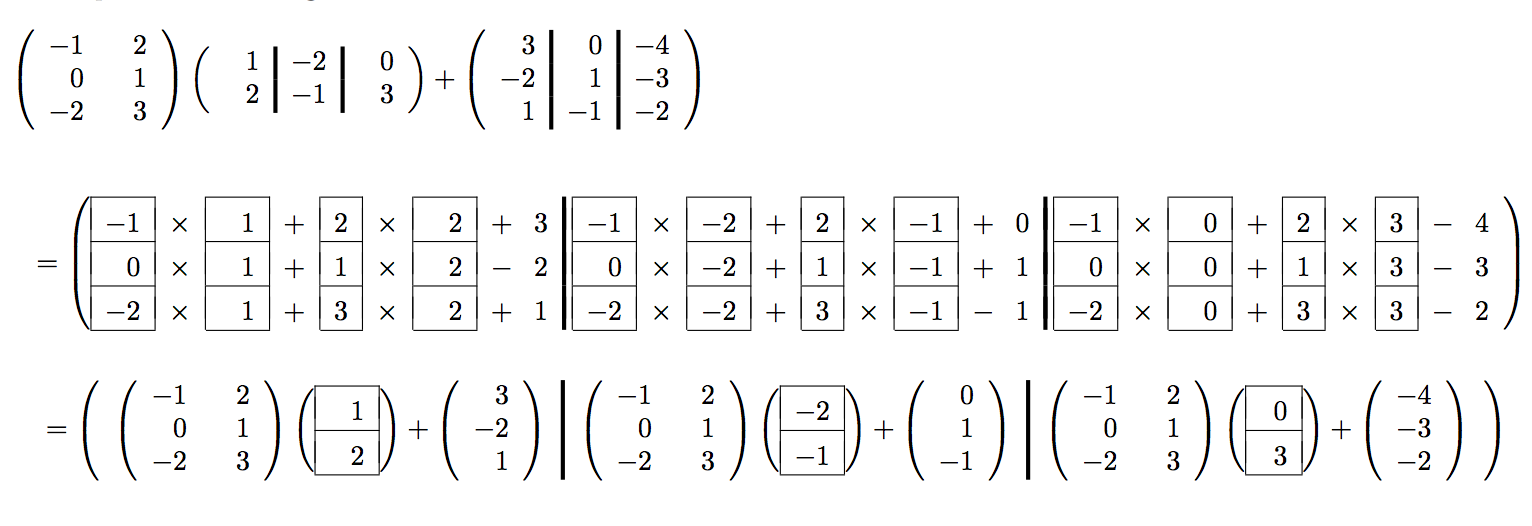Skip to main content

Unit 1.3.6 Matrix-matrix multiplication via matrix-vector multiplications

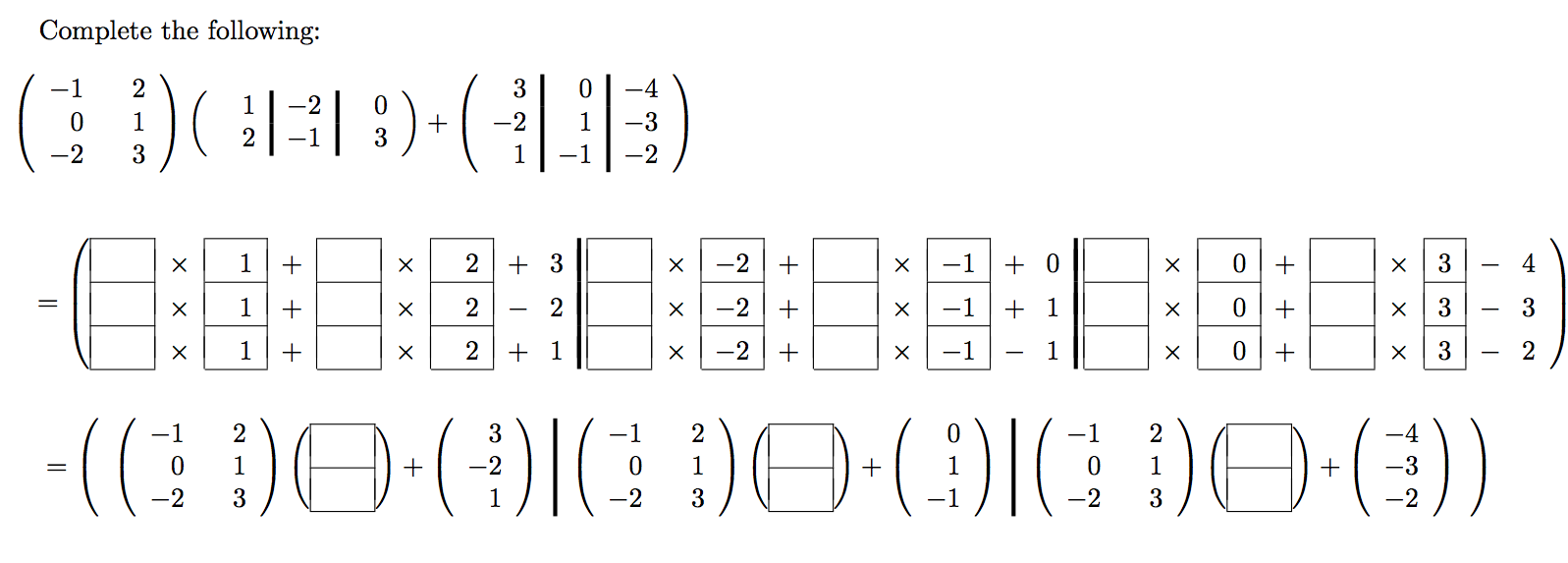
Now that we are getting comfortable with partitioning matrices and vectors, we can view the six algorithms for \(C := A B + C \) in a more layered fashion. If we partition \(C \) and \(B \) by columns, we find that

\begin{equation*} \begin{array}{rcl} \left( \begin{array}{c | c | c | c } c_0 \amp c_1 \amp \cdots \amp c_{n-1} \end{array} \right) \amp:=\amp A \left( \begin{array}{c | c | c | c } b_0 \amp b_1 \amp \cdots \amp b_{n-1} \end{array} \right) + \left( \begin{array}{c | c | c | c } c_0 \amp c_1 \amp \cdots \amp c_{n-1} \end{array} \right) \\ \amp = \amp \left( \begin{array}{c | c | c | c } A b_0 + c_0 \amp A b_1 + c_1 \amp \cdots \amp A b_{n-1} + c_{n-1} \end{array} \right) \end{array} \end{equation*}

A picture that captures this is given by

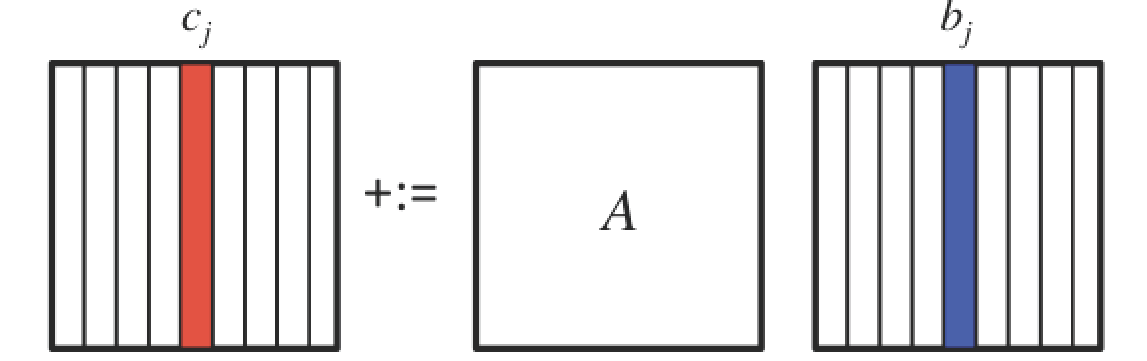
This illustrates how the JIP and JPI algorithms can be layered as a loop around matrix-vector multiplications, which itself can be layered as a loop around dot products or axpy operations:

\begin{equation*} \begin{array}{l} {\bf for~} j := 0, \ldots , n-1 \\[0.15in] ~~~ \left. \begin{array}{l} {\bf for~} p := 0, \ldots , k-1 \\[0.15in] ~~~ ~~~ \left. \begin{array}{l} {\bf for~} i := 0, \ldots , m-1 \\ ~~~ ~~~ \gamma_{i,j} := \alpha_{i,p} \beta_{p,j} + \gamma_{i,j} \\ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{c_j := \beta_{p,j} a_p + c_j}\\ \mbox{axpy} \end{array} \\[0.2in] ~~~ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{c_j := A b_j + c_j}\\ \mbox{mv mult} \end{array} \\[0.2in] {\bf end} \end{array} \end{equation*}

and

\begin{equation*} \begin{array}{l} {\bf for~} j := 0, \ldots , n-1 \\[0.15in] ~~~ \left. \begin{array}{l} {\bf for~} i := 0, \ldots , m-1 \\[0.15in] ~~~ ~~~ \left. \begin{array}{l} {\bf for~} p := 0, \ldots , k-1 \\ ~~~ ~~~ \gamma_{i,j} := \alpha_{i,p} \beta_{p,j} + \gamma_{i,j} \\ {\bf end} \end{array} \right\} ~~~ \gamma_{i,j} := \begin{array}[t]{c} \underbrace{ \widetilde a_i^T b_j + \gamma_{i,j}} \\ \mbox{dots} \end{array} \\[0.2in] ~~~ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{c_j := A b_j + c_j}\\ \mbox{mv mult} \end{array} \\[0.2in] {\bf end} \end{array} \end{equation*}
Remark 1.3.6.

The file name Gemm_J_Gemv.c can be decoded as follows:

  • The Gemm stands for "GEneral Matrix-Matrix multiplication."

  • The J indicates a loop indexed by \(j\) (a loop over columns of matrix \(C\)).

  • The Gemv indicates that the operation performed in the body of the loop is matrix-vector multiplication.

Similarly, J_Gemv_I_Dots means that the implementation of matrix-matrix multiplication being compiled and executed consists of a loop indexed by \(j\) (a loop over the columns of matrix \(C\)) which itself calls a matrix-vector multiplication that is implemented as a loop indexed by \(i\) (over the rows of the matrix with which the matrix-vector multiplication is performed), with a dot product in the body of the loop.

Remark 1.3.7.

Hopefully you are catching on to our naming convention. It is a bit adhoc and we are probably not completely consistent. They give some hint as to what the implementation looks like.

Going forward, we refrain from further explaining the convention.

login