Skip to main content

Unit 3.1.1 Launch

Remark 3.1.1.

As you may have noticed, some of the programming assignments are still in flux. This means

  • You will want to do 

    git stash save
git pull
git stash pop

    in your LAFF-On-PfHP directory.

  • You will want to upload the .mlx files form LAFF-On-PfHP.Assignments/Week3/C/data/ to the corresponding folder of Matlab Online.

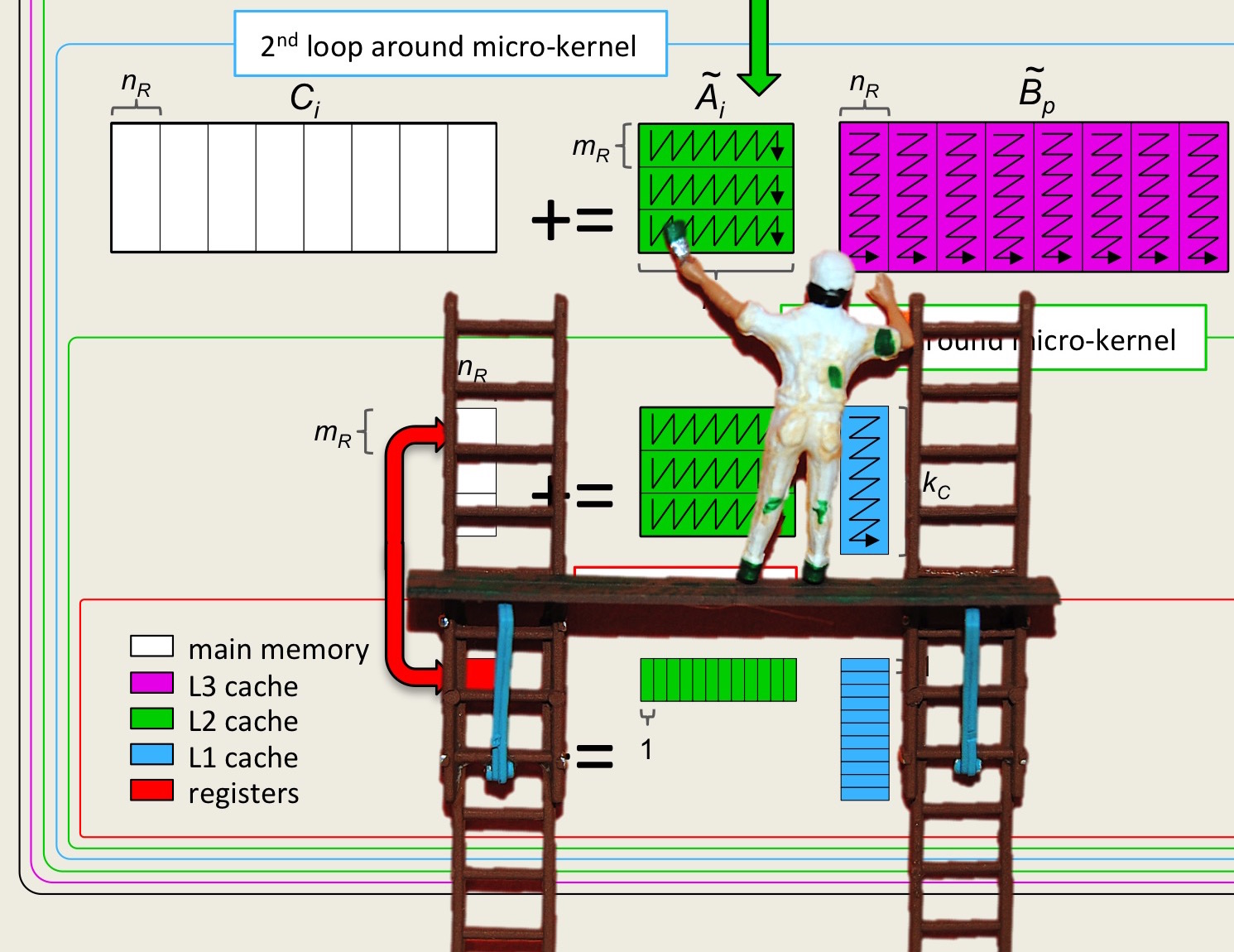
The inconvenient truth is that floating point computations can be performed very fast while bringing data in from main memory is relatively slow. How slow? On a typical architecture it takes two orders of magnitude more time to bring a floating point number in from main memory than it takes to compute with it.

The reason why main memory is slow is relatively simple: there is not enough room on a chip for the large memories that we are accustomed to and hence they are off chip. The mere distance creates a latency for retrieving the data. This could then be offset by retrieving a lot of data simultaneously, increasing bandwidth. Unfortunately there are inherent bandwidth limitations: there are only so many pins that can connect the central processing unit (CPU) with main memory.

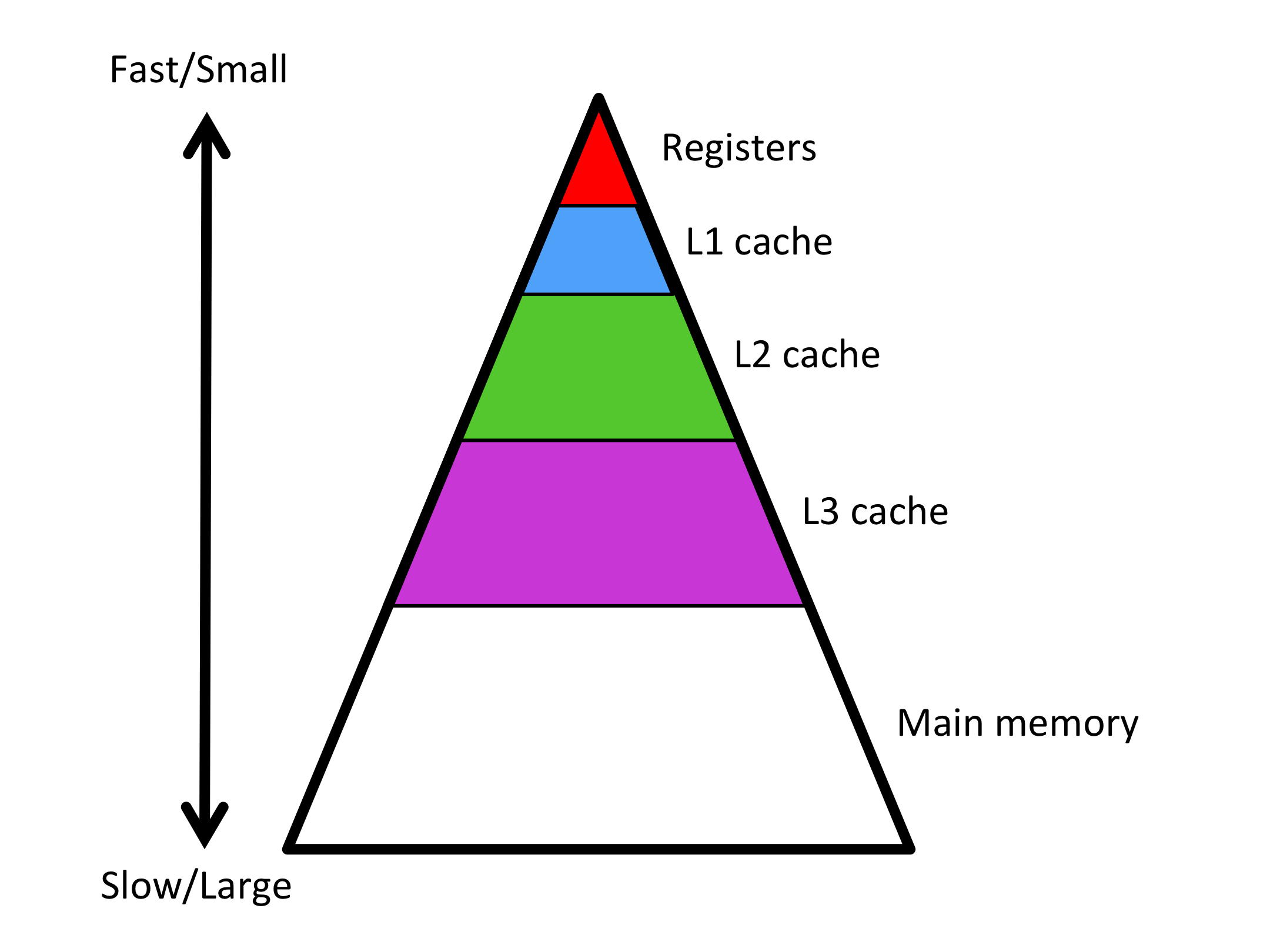
Figure 3.1.2. Illustration of the memory hierarchy.

To overcome this limitation, a modern processor has a hierarchy of memories. We have already encountered the two extremes: registers and main memory. In between, there are smaller but faster cache memories. These cache memories are on-chip and hence do not carry the same latency as does main memory and also can achieve greater bandwidth. The hierarchical nature of these memories is often depicted as a pyramid as illustrated in Figure 3.1.2.

To put things in perspective: We have discussed that a core on the kind of modern CPU we target in this course has sixteen vector registers that can store 4 double precision floating point numbers (doubles) each, for a total of 64 doubles. Built into the CPU it has a 32Kbytes level-1 cache (L1 cache) that can thus store 4,096 doubles. Somewhat further it has a 256Kbytes level-2 cache (L2 cache) that can store 32,768 doubles. Further away yet, but still on chip, it has an 8Mbytes level-3 cache (L3 cache) that can hold 1,048,576 doubles.

Remark 3.1.3.

In further discussion, we will pretend that one can place data in a specific cache and keep it there for the duration of computations. In fact, caches retain data using some cache replacement policy that evicts data that has not been recently used. By carefully ordering computations, we can encourage data to remain in cache, which is what happens in practice.

You may want to read up on cache replacement policies on Wikipedia: https://en.wikipedia.org/wiki/Cache_replacement_policies.

Homework 3.1.1.1.

Since we compute with (sub)matrices, it is useful to have some idea of how big of a matrix one can fit in each of the layers of cache. Assuming each element in the matrix is a double precision number, which requires 8 bytes, complete the following table:

\begin{equation*} \begin{array}{| c | r | l |}\hline {\rm Layer} \amp {\rm Size} \amp {\rm Largest~} n \times n {\rm ~matrix} \\ \hline {\rm Registers} \amp 16 \times 4 {\rm ~doubles} \amp n = ~~~~~~~~~~~ \\ \hline {\rm L1~cache}\amp 32 {\rm ~Kbytes} \amp n = ~~~~~~~~~~~ \\ \hline {\rm L2~cache} \amp 256 {\rm ~Kbytes} \amp n = ~~~~~~~~~~~ \\ \hline {\rm L3~cache} \amp 8 {\rm ~Mbytes} \amp n = ~~~~~~~~~~~~~~~~~~~~~~ \\ \hline {\rm Main~Memory} \amp 16 {\rm ~Gbytes} \amp n = ~~~~~~~~~~~~~~~~~~~~~~ \\ \hline \end{array} \end{equation*}
Solution
\begin{equation*} \begin{array}{| c | r | l |}\hline {\rm Layer} \amp {\rm Size} \amp {\rm Largest~} n \times n {\rm ~matrix} \\ \hline {\rm Registers} \amp 16 \times 4 {\rm ~doubles} \amp n = \sqrt{ 64 } = 8 \\ \hline {\rm L1~cache}\amp 32 {\rm ~Kbytes} \amp n = \sqrt{32 \times 1024 / 8} = 64 \\ \hline {\rm L2~cache} \amp 256 {\rm ~Kbytes} \amp n = \sqrt{ 256 \times 1024 / 8 } = 181 \\ \hline {\rm L3~cache} \amp 8 {\rm ~Mbytes} \amp n = \sqrt{ 8 \times 1024 \times 1024/ 8 } = 1024 \\ \hline {\rm Main~memory} \amp 16 {\rm ~Gbytes} \amp n = \sqrt{ 16 \times 1024 \times 1024 \times 1024/ 8 } \approx 46,341 \\ \hline \end{array} \end{equation*}

login