Skip to main content

Unit 3.3.4 Implementation: packing block \(A_{i,p} \)

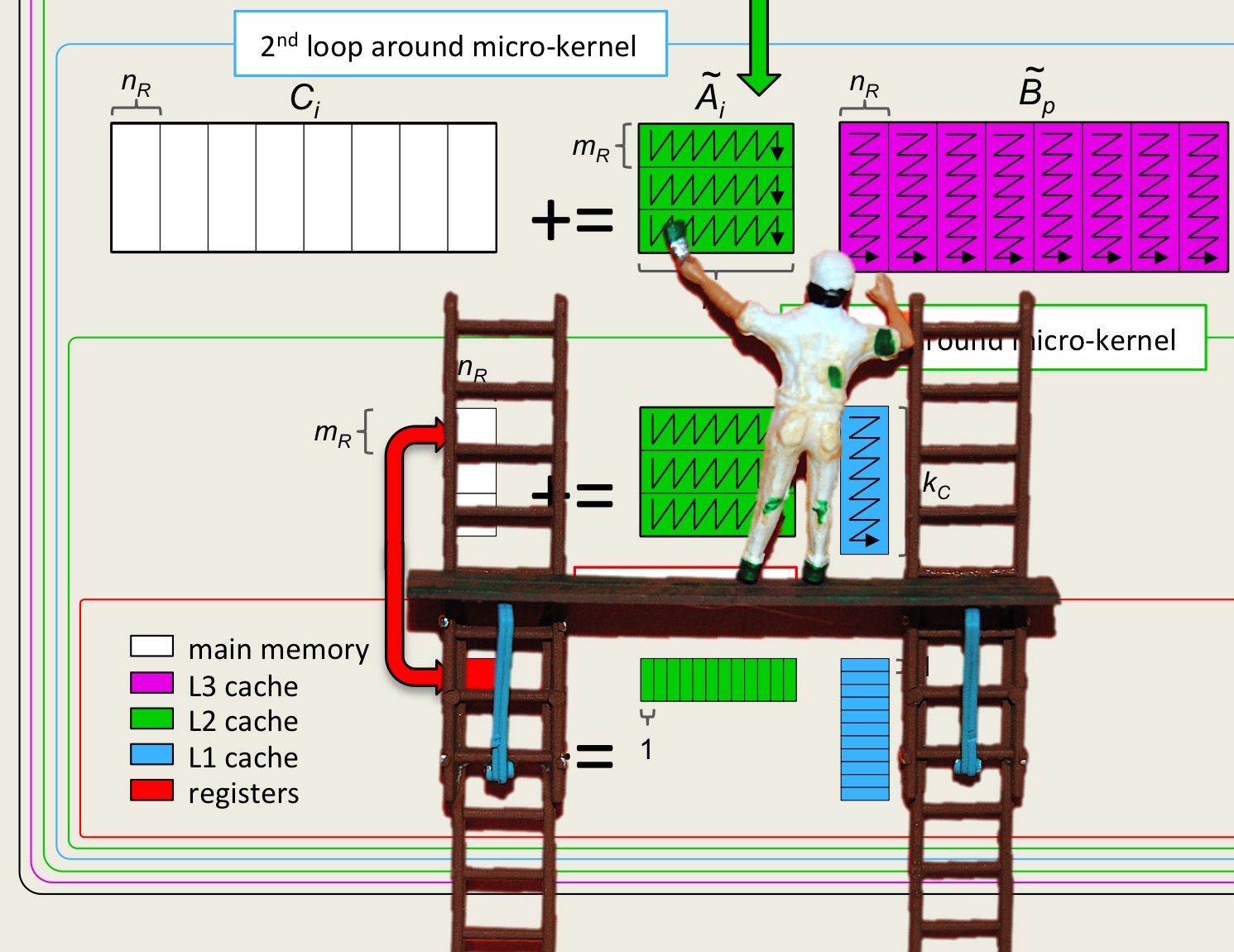
We next discuss the packing of the block \(A_{i,p} \) into \(\widetilde A_{i,p} \text{:}\)

We break the implementation, in Assignments/Week3/C/PackA.c, down into two routines. The first loops over all the rows that need to be packed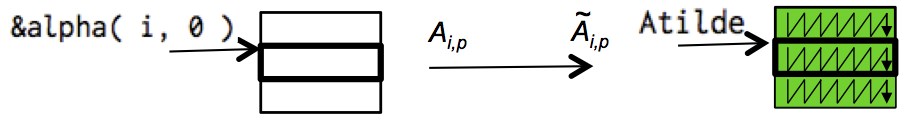

as illustrated in Figure 3.3.5.

void PackBlockA_MCxKC( int m, int k, double *A, int ldA, double *Atilde ) 
/* Pack a  m x k block of A into a MC x KC buffer.   MC is assumed to
    be a multiple of MR.  The block is packed into Atilde a micro-panel
    at a time. If necessary, the last micro-panel is padded with rows
    of zeroes. */
{
  for ( int i=0; i<m; i+= MR ){
    int ib = min( MR, m-i );

    PackMicro-PanelA_MRxKC( ib, k, &alpha( i, 0 ), ldA, Atilde );
    Atilde += ib * k;
  }
}

Figure 3.3.5. A reference implementation for packing \(A_{i,p} \text{.}\)

That routine then calls a routine that packs the panel

Given in Figure 3.3.6.

void PackMicroPanelA_MRxKC( int m, int k, double *A, int ldA, double *Atilde ) 
/* Pack a micro-panel of A into buffer pointed to by Atilde. 
   This is an unoptimized implementation for general MR and KC. */
{
  /* March through A in column-major order, packing into Atilde as we go. */

  if ( m == MR ) {
    /* Full row size micro-panel.*/
    for ( int p=0; p<k; p++ ) 
      for ( int i=0; i<MR; i++ ) 
        *Atilde++ = alpha( i, p );
  }
  else {
    /* Not a full row size micro-panel.  We pad with zeroes.  To be  added */
  }
}

Figure 3.3.6. A reference implementation for packing a micro-panel of \(A_{i,p} \text{.}\)
Remark 3.3.7.

Again, these routines only work when the sizes are "nice". We leave it as a challenge to generalize all implementations so that matrix-matrix multiplication with arbitrary problem sizes works. To manage the complexity of this, we recommend "padding" the matrices with zeroes as they are being packed. This then keeps the micro-kernel simple.

login