Skip to main content

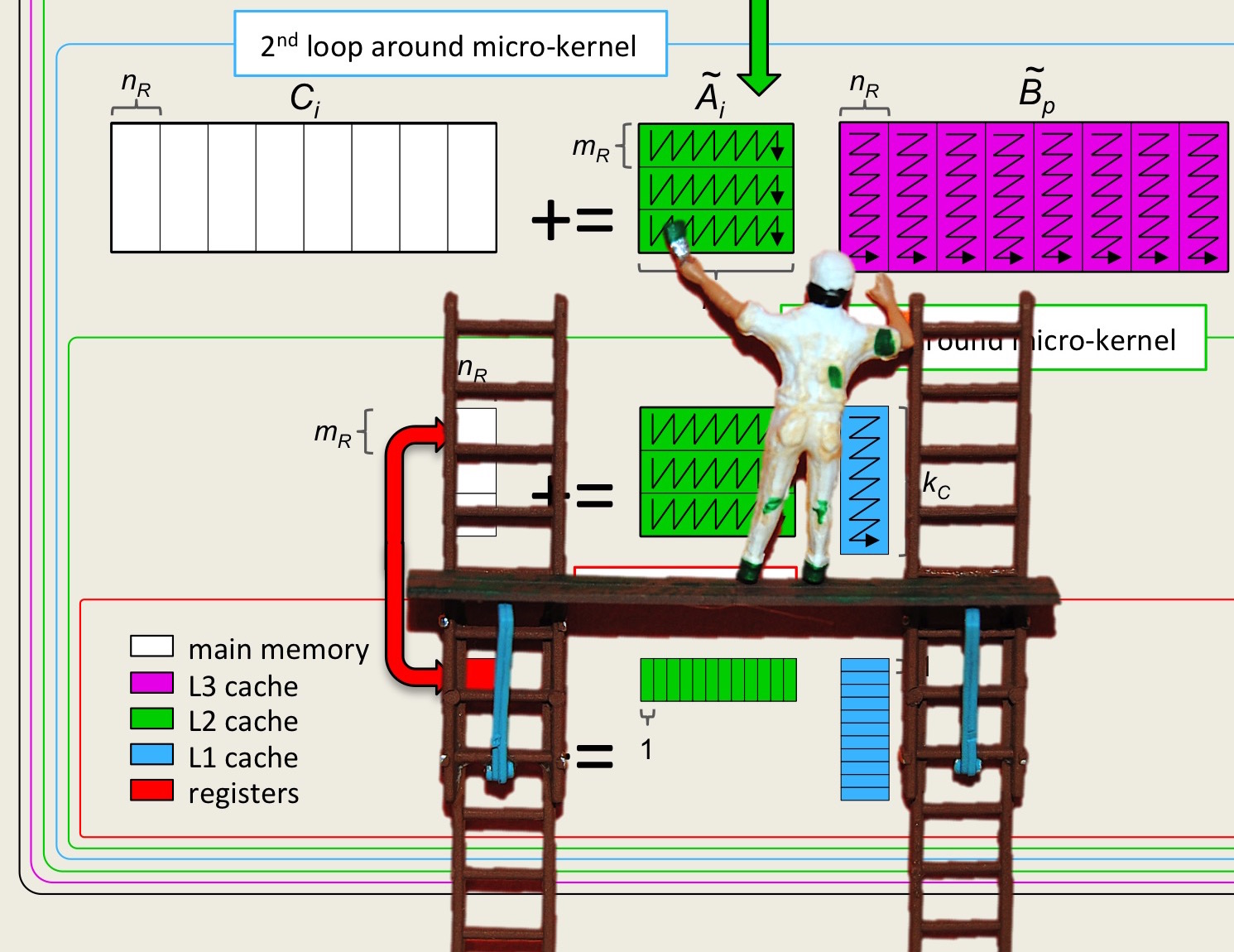
Unit 4.3.5 Parallelizing the fourth loop around the micro-kernel

Next, consider how to parallelize the fourth loop around the micro-kernel:

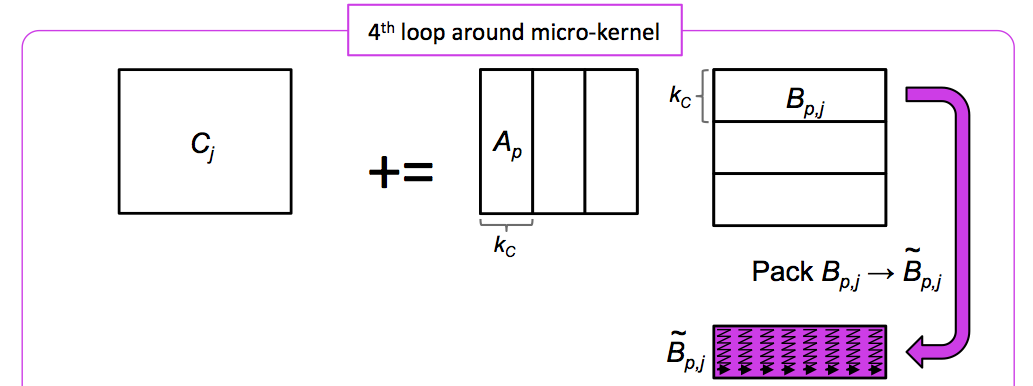
We can describe this picture by partitioning \(A\) into column panels and \(B\) into row panels:

\begin{equation*} C := \left( \begin{array}{c| c | c} A_0 \amp \cdots \amp A_{m-1} \end{array} \right) \left( \begin{array}{c} B_0 \\ \hline \vdots \\ \hline B_{m-1} \end{array} \right) + C = A_0 B_0 + \cdots + A_{K-1} B_{K-1} + C. \end{equation*}

Given, for example, four threads, the thread with id \(0\) can compute

\begin{equation*} A_0 B_0 + A_4 B_4 + \cdots + C \end{equation*}

while the thread with id \(1\) computes

\begin{equation*} A_1 B_1 + A_5 B_5 + \cdots + \end{equation*}

and so forth.

Homework 4.3.5.1.

In directory Assignments/Week4/C,

  • Copy Gemm_MT_Loop3_MRxNRKernel.c. into Gemm_MT_Loop4_MRxNRKernel.c.

  • Modify it so that only the fourth loop around the micro-kernel is parallelized.

  • Execute it with 

    export OMP_NUM_THREADS=4
make MT_Loop4_8x6Kernel

  • Be sure to check if you got the right answer! Parallelizing this loop is a bit trickier... Even trickier than parallelizing the third loop around the micro-kernel... Don't spend too much time on it before looking at the hint.

  • View the resulting performance with data/Plot_MT_performance_8x6.mlx, uncommenting the appropriate sections.

Hint

Initially you may think that parallelizing this is a matter of changing how the temporary space \(\widetilde B\) is allocated and used. But then you find that even that doesn't give you the right answer... The problem is that all iterations update the same part of \(C\) and this creates something called a "race" condition. To update \(C\text{,}\) you read a micro-tile of \(C\) into registers, you update it, and you write it out. What if in the mean time another thread reads the same micro-tile of \(C\text{?}\) It would be reading the old data...

The fact is that Robert has yet to find the courage to do this homework himself... Perhaps you too should skip it.

Solution

I have no solution to share at this moment...

The problem is that in the end all these contributions need to be added for the final result. Since all threads update the same array in which \(C \) is stored, then you never know if a given thread starts updating an old copy of a micro-tile of \(C\) while another thread is still updating it. This is known as a race condition.

This doesn't mean it can't be done, nor that it isn't worth pursuing. Think of a matrix-matrix multiplication where \(m \) and \(n\) are relatively small and \(k\) is large. Then this fourth loop around the micro-kernel has more potential for parallelism than the other loops. It is just more complicated and hence should wait until you learn more about OpenMP (in some other course).

login