

ACL2 !>(app nil '(x y z)) (X Y Z)ACL2 !>(app '(1 2 3) '(4 5 6 7)) (1 2 3 4 5 6 7)
ACL2 !>(app '(a b c d e f g) '(x y z)) ; click here for an explanation (A B C D E F G X Y Z)
ACL2 !>(app (app '(1 2) '(3 4)) '(5 6)) (1 2 3 4 5 6)
ACL2 !>(app '(1 2) (app '(3 4) '(5 6))) (1 2 3 4 5 6)
ACL2!>(let ((a '(1 2)) (b '(3 4)) (c '(5 6))) (equal (app (app a b) c) (app a (app b c)))) T

As we can see from these examples, ACL2 functions can be executed more or less as Common Lisp.
The last three examples suggest an interesting property of app.
Induction on a is unflawed: every occurrence of a in the conjecture
(equal (app (app a b) c)
(app a (app b c)))
is in a position being recursively decomposed!
Now look at the occurrences of b. The first (shown in bold below)
is in a position that is held constant in the recursion of (app a b).
It would be ``bad'' to induct on b here.
(equal (app (app a b) c)
(app a (app b c)))


Consider a typical ``stack'' of control frames.
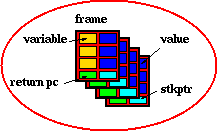
Suppose the model required that we express the idea of ``the most recent
frame whose return program counter points into MAIN.''
The natural expression of this notion involves
function application -- ``fetch the return-pc of this frame''
case analysis -- ``if the pc is MAIN, then ...''
iteration or recursion -- ``pop this frame off and repeat.''
The designers of ACL2 have taken the position that a programming language is the natural language in which to define such notions, provided the language has a mathematical foundation so that models can be analyzed and properties derived logically.
 is the language supported by ACL2.
Click here for an optional and very brief introduction
to Common Lisp.
is the language supported by ACL2.
Click here for an optional and very brief introduction
to Common Lisp.
Common Lisp functions are partial; they are not defined for all possible inputs. But ACL2 functions are total. Roughly speaking, the logical function of a given name in ACL2 is a completion of the Common Lisp function of the same name obtained by adding some arbitrary but ``natural'' values on arguments outside the ``intended domain'' of the Common Lisp function.
ACL2 requires that every ACL2 function symbol have a ``guard,''
which may be thought of as a predicate on the formals of the
function describing the intended domain. The guard on the primitive
function car  , for example, is
, for example, is (or (consp x) (equal x nil)),
which requires the argument to be either an ordered pair or
nil. We will discuss later how to specify a guard for a
defined function; when one is not specified, the guard is t which
is just to say all arguments are allowed.
But guards are entirely extra-logical: they are not involved in the axioms defining functions. If you put a guard on a defined function, the defining axiom added to the logic defines the function on all arguments, not just on the guarded domain.
So what is the purpose of guards?
The key to the utility of guards is that we provide a mechanism, called ``guard verification,'' for checking that all the guards in a formula are true. That is,(i-am-here)
Functions in ACL2 may restrict their arguments. These restrictions
take the form of formulas about the formal parameters. These
formulas are called ``guards.'' The Common Lisp primitives such as
car  and
and endp  have guards. ACL2 permits you to
specify restrictions on the arguments to the functions you define.
To do so you use the
have guards. ACL2 permits you to
specify restrictions on the arguments to the functions you define.
To do so you use the xargs  declaration (see declare
declaration (see declare
 ) for
) for defun  .
.
Logically speaking, guards are irrelevant. (i-am-here)


When a function is admitted to the logic, ACL2 tries to ``guess''
what type of object it returns. This guess is codified as a term
that expresses a property of the value of the function. For app
the term is
(OR (CONSP (APP X Y))
(EQUAL (APP X Y) Y))
which says that app returns either a cons or its second argument.
This formula is added to ACL2's rule base as a type-prescription
 rule. Later we will discuss how rules are used by the ACL2
theorem prover. The point here is just that when you add a definition,
the data base of rules is updated, not just by the addition of the
definitional axiom, but by several new rules.
rule. Later we will discuss how rules are used by the ACL2
theorem prover. The point here is just that when you add a definition,
the data base of rules is updated, not just by the addition of the
definitional axiom, but by several new rules.
You should now return to the Walking Tour.


Now that you have seen the theorem prover in action you might be curious as to how you guide it.
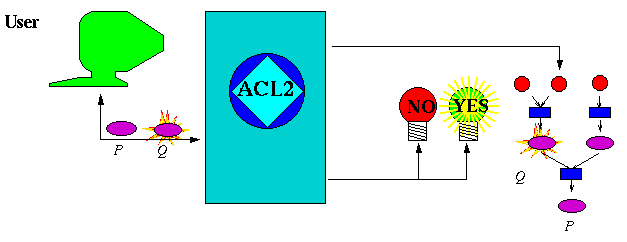
The idea is that the user submits conjectures and advice and reads the proof attempts as they are produced.
Most of the time, the conjectures submitted are lemmas to be used in the proofs of other theorems.
The example
ACL2 !>(app 7 27)illustrates the fact that while ACL2 is an untyped language the ACL2 evaluator can be configured so as to check ``types'' at runtime. We should not say ``types'' here but ``guards.'' Click here for a discussion of guards.ACL2 Error in TOP-LEVEL: The guard for the function symbol ENDP, which is (OR (CONSP X) (EQUAL X NIL)), is violated by the arguments in the call (ENDP 7).
The guard on endp  requires its argument to be a true
list. Since 7 is not a true list, and since ACL2 is checking guards
in this example, an error is signaled by ACL2. How do you know
ACL2 is checking guards? Because the prompt tells us
(click here) with its ``!''.
requires its argument to be a true
list. Since 7 is not a true list, and since ACL2 is checking guards
in this example, an error is signaled by ACL2. How do you know
ACL2 is checking guards? Because the prompt tells us
(click here) with its ``!''.


The training time depends primarily on the background of the user.
We expect that a user who
* has a bachelor's degree in computer science or mathematics,will probably take several months to become an effective ACL2 user.* has some experience with formal methods,
* has had some exposure to Lisp programming and is comfortable with the Lisp notation,
* is familiar with and has unlimited access to a Common Lisp host processor, operating system, and text editor (we use Sun workstations running Unix and GNU Emacs),
* is willing to read and study the ACL2 documentation, and
* is given the opportunity to start with ``toy'' projects before being expected to tackle the company's Grand Challenge,
Most ACL2 primitives are documented. Here is the definition of
app again, with the documented topics highlighted.  All of the
links below lead into the ACL2 online documentation, 1.5 megabytes of
hyperlinked text. So follow these links around, but remember to come
back here!
All of the
links below lead into the ACL2 online documentation, 1.5 megabytes of
hyperlinked text. So follow these links around, but remember to come
back here!
(defun app (x y)
(cond ((endp x) y)
(t (cons (car x)
(app (cdr x) y)))))
By following the link on endp  we see that it is a
Common Lisp function and is defined to be the same as atom
we see that it is a
Common Lisp function and is defined to be the same as atom
 , which recognizes non-conses. But
, which recognizes non-conses. But endp has a guard.
Since we are ignorning guards for now, we'll ignore the guard issue
on endp.
So this definition reads ``to app x and y: if x is an
atom, return y; otherwise, app (cdr x) and y and then
cons (car x) onto that.''
You can always use the Index  to find the documentation of
functions. Try it. Click on the Index icon below. Then use the
Find command of your browser to find ``endp'' in that document and
follow the link. But remember to come back here.
to find the documentation of
functions. Try it. Click on the Index icon below. Then use the
Find command of your browser to find ``endp'' in that document and
follow the link. But remember to come back here.
The ACL2 documentation is also available via Emacs' TexInfo, allowing you to explore the hyperlinked documentation in the comfort of a text editor that can also interact with ACL2.
In addition, some runtime images of ACL2 (the so-called ``large image'') have the hyperlinked text as a large ACL2 data structure that can be explored with ACL2's :doc command. If you have ACL2 running, try the command :doc endp. If that doesn't work, you are running the ``small image.''
Another way to find out about ACL2 functions, if you have an ACL2
image available, is to use the command :args  which
prints the formals, type, and guard of a function symbol.
which
prints the formals, type, and guard of a function symbol.
Of course, the ACL2 documentation can also be printed out as 700 page book. See the ACL2 Home Page to download the Postscript.
Now let's continue with app.
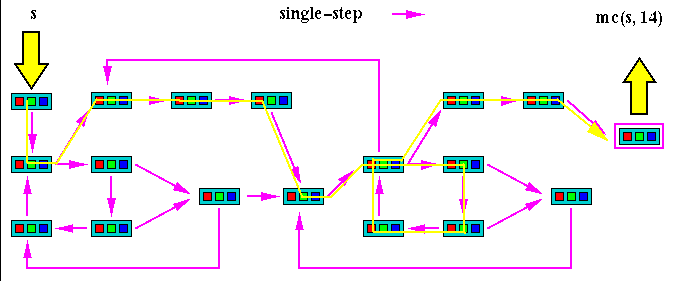
Below we define mc(s,n) to be the function that single-steps n
times from a given starting state, s.
In Common Lisp, ``mc(s,n)'' is written (mc s n).
(defun mc (s n) ; To step s n times:
(if (zp n) ; If n is 0
s ; then return s
(mc (single-step s) (- n 1)))) ; else step single-step(s)
n-1 times.
This is an example of a formal model in ACL2.
Frequently, engineers use mathematical models. Use of such models frequently lead to
better designs,
faster completion of acceptable products, and
reduced overall cost,
because models allow the trained user to study the design before it is built and analyze its properties. Usually, testing and analyzing a model is cheaper and faster than fabricating and refabricating the product.
Click here to continue.


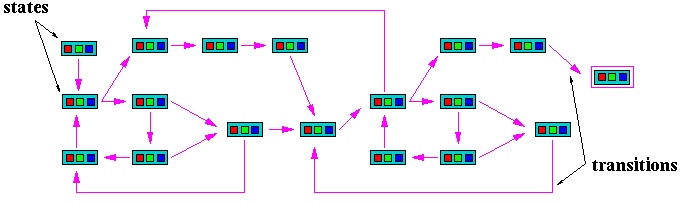
Computing machines, whether hardware or software or some combintation, are frequently modeled as ``state machines.''
To so model a computing machine we must represent its states as objects in our mathematical framework.
Transitions are functions or relations on state objects.
In what language shall we define these objects, functions, and relations?
The mathematical languages we were taught in high school
algebra,
geometry,
trignometry, and
calculus
are inappropriate for modeling digital systems. They primarily let us talk about numbers and continuous functions.
To see what kind of expressive power we need, take a closer look at what a typical state contains.
When the theorem prover explicitly assigns a name, like *1, to a
formula, it has decided to prove the formula by induction.


The numbers in ACL2 can be partitioned into the following subtypes:
Rationals Integers Positive integers3Zero0Negative Integers-3Non-Integral Rationals Positive Non-Integral Rationals19/3Negative Non-Integral Rationals-22/7Complex Rational Numbers#c(3 5/2) ; = 3+(5/2)i
Signed integer constants are usually written (as illustrated above)
as sequences of decimal digits, possibly preceded by + or -.
Decimal points are not allowed. Integers may be written in binary,
as in #b1011 (= 23) and #b-111 (= -7). Octal may also be
used, #o-777 = -511. Non-integral rationals are written as a
signed decimal integer and an unsigned decimal integer, separated by
a slash. Complex rationals are written as #c(rpart ipart) where
rpart and ipart are rationals.
Of course, 4/2 = 2/1 = 2 (i.e., not every rational written with a slash is a non-integer). Similarly, #c(4/2 0) = #c(2 0) = 2.
The common arithmetic functions and relations are denoted by +,
-, *, /, =, <, <=, > and >=. However there
are many others, e.g., floor, ceiling, and lognot. We
suggest you see programming  where we list all of the primitive
ACL2 functions. Alternatively, see any Common Lisp language
documentation.
where we list all of the primitive
ACL2 functions. Alternatively, see any Common Lisp language
documentation.
The primitive predicates for recognizing numbers are illustrated below. The following ACL2 function will classify an object, x, according to its numeric subtype, or else return 'NaN (not a number). We show it this way just to illustrate programming in ACL2.
(defun classify-number (x)
(cond ((rationalp x)
(cond ((integerp x)
(cond ((< 0 x) 'positive-integer)
((= 0 x) 'zero)
(t 'negative-integer)))
((< 0 x) 'positive-non-integral-rational)
(t 'negative-non-integral-rational)))
((complex-rationalp x) 'complex-rational)
(t 'NaN)))


Subgoal *1/2 is the induction step from the scheme, obtained by
instantiating the scheme with our conjecture.
We number the cases ``backward'', so this is case ``2'' of the
proof of ``*1''. We number them backward so you can look at a subgoal
number and get an estimate for how close you are to the end.


ACL2 is distributed on the Web without fee.
There is a License agreement, which is available via the ACL2 Home Page link below.
ACL2 currently runs on the Unix, Linux, and Macintosh operating systems.
It can be built in any of the following Common Lisps:
* Allegro, * GCL (Gnu Common Lisp) [or, AKCL], * Lispworks, * Lucid, and * MCL (Macintosh Common Lisp).
We recommend running ACL2 with at least 16MB of memory and prefer significantly more (e.g., 64MB).
Subgoal *1/1 is the Base Case of our induction. It
simplifies to Subgoal *1/1' by expanding the ENDP term in the
hypothesis, just as we saw in the earlier proof of Subgoal *1/2.


In this message the system is saying that Subgoal *1/2 has been
rewritten to the Subgoal *1/2', by expanding the definition of endp.
This is an example of simplification, one of the main proof
techniques used by the theorem prover.
Click here if you would like to step through the
simplification of Subgoal *1/2.


The But is our signal that the goal is proved.
Click here to step through the proof. It is very simple.



ACL2 !>(defthm trivial-consequence
(equal (app (app (app (app x1 x2) (app x3 x4)) (app x5 x6)) x7)
(app x1 (app (app x2 x3) (app (app x4 x5) (app x6 x7))))))
ACL2 Warning [Subsume] in ( DEFTHM TRIVIAL-CONSEQUENCE ...): The previously
added rule ASSOCIATIVITY-OF-APP subsumes the newly proposed :REWRITE
rule TRIVIAL-CONSEQUENCE, in the sense that the old rule rewrites a
more general target. Because the new rule will be tried first, it
may nonetheless find application.
By the simple :rewrite rule ASSOCIATIVITY-OF-APP we reduce the conjecture
to
Goal'
(EQUAL (APP X1
(APP X2
(APP X3 (APP X4 (APP X5 (APP X6 X7))))))
(APP X1
(APP X2
(APP X3 (APP X4 (APP X5 (APP X6 X7))))))).
But we reduce the conjecture to T, by primitive type reasoning.
Q.E.D.
Summary
Form: ( DEFTHM TRIVIAL-CONSEQUENCE ...)
Rules: ((:REWRITE ASSOCIATIVITY-OF-APP)
(:FAKE-RUNE-FOR-TYPE-SET NIL))
Warnings: Subsume
Time: 0.20 seconds (prove: 0.02, print: 0.00, other: 0.18)
TRIVIAL-CONSEQUENCE

You might explore the links before moving on.
Subgoal *1/1
(IMPLIES (ENDP A)
(EQUAL (APP (APP A B) C)
(APP A (APP B C)))).
By the simple :definition ENDP we reduce the conjecture to
Subgoal *1/1'
(IMPLIES (NOT (CONSP A))
(EQUAL (APP (APP A B) C)
(APP A (APP B C)))).
But simplification reduces this to T, using the :definition APP and
primitive type reasoning.
In this message the system is saying that Subgoal *1/2' has been
rewritten T using the rules noted. The word ``But'' at the
beginning of the sentence is a signal that the goal has been proved.
Click here to step through the proof of Subgoal *1/2'.


Subgoal *1/2
(IMPLIES (AND (NOT (ENDP A))
(EQUAL (APP (APP (CDR A) B) C)
(APP (CDR A) (APP B C))))
(EQUAL (APP (APP A B) C)
(APP A (APP B C)))).
By the simple :definition ENDP we reduce the conjecture to
Subgoal *1/2'
(IMPLIES (AND (CONSP A)
(EQUAL (APP (APP (CDR A) B) C)
(APP (CDR A) (APP B C))))
(EQUAL (APP (APP A B) C)
(APP A (APP B C)))).
But simplification reduces this to T, using the :definition APP, the
:rewrite rules CDR-CONS and CAR-CONS and primitive type reasoning.
The theorem prover's proof is printed in real time. At the time it
prints ``Perhaps'' it does not know the proof will succeed.


Recall that our induction scheme (click here to revisit it)
had two cases, the induction step (Subgoal *1/2) and the base
case (Subgoal *1/1). Both have been proved!


But ACL2 is a logic. We can prove theorems about the model.
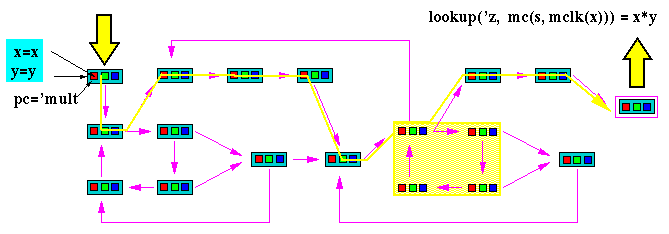
Theorem. MC 'mult is a multiplier
(implies (and (natp x)
(natp y))
(equal (lookup 'z (mc (s 'mult x y) (mclk x)))
(* x y))).
This theorem says that a certain program running on the mc machine will correctly multiply any two natural numbers.
It is a statement about an infinite number of test cases!
We know it is true about the model because we proved it.
Here is the
definition of app again with certain parts highlighted. If you
are taking the Walking Tour, please read the text carefully and
click on each of the links below, except those marked  .
Then come back here.
.
Then come back here.

ACL2 !>(defun app (x y)
(cond ((endp x) y)
(t (cons (car x)
(app (cdr x) y)))))
The admission of APP is trivial, using the
relation E0-ORD-<  (which is known to be well-founded on
the domain recognized by E0-ORDINALP
(which is known to be well-founded on
the domain recognized by E0-ORDINALP  ) and the measure
(ACL2-COUNT
) and the measure
(ACL2-COUNT  X). We observe that the
type of APP is described by the theorem (OR
(CONSP (APP X Y)) (EQUAL (APP X Y) Y)). We used primitive type
reasoning.
X). We observe that the
type of APP is described by the theorem (OR
(CONSP (APP X Y)) (EQUAL (APP X Y) Y)). We used primitive type
reasoning.
Summary
Form: ( DEFUN APP ...)
Rules: ((:FAKE-RUNE-FOR-TYPE-SET NIL))
Warnings: None
Time: 0.03 seconds (prove: 0.00, print: 0.00, other: 0.03)
APP

By reading the documentation of defthm  (and
especially of its :rule-classes
(and
especially of its :rule-classes  argument)
you would learn that
when we submitted the command
argument)
you would learn that
when we submitted the command
(defthm associativity-of-app
(equal (app (app a b) c)
(app a (app b c))))
we not only command the system to prove that app is an associative
function but
* we commanded it to use that fact as a rewrite rule.
That means that every time the system encounters a term of the form
(app (app x y) z)it will replace it with
(app x (app y z))!
Suppose the machine being modeled is some kind of arithmetic unit. Suppose the model can be initialized so as to multiply x times y and leave the answer in z. Then if we initialize s to multiply with x=5 and y=7 and run the machine long enough, we can read the answer 35 in the final state.
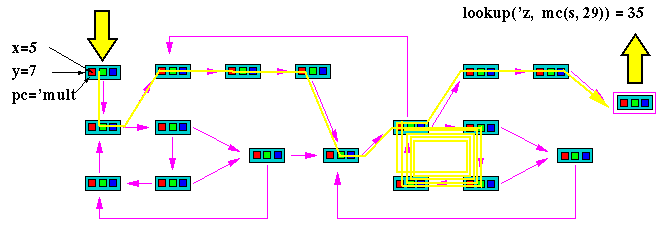
Because ACL2 is a programming language, our model can be run or executed.
If you defined the model in ACL2 and then typed
> (lookup 'z (mc (s 'mult 5 7) 29))
then ACL2 would compute 35. You can emulate or test the model of your machine.
This is obvious because ACL2 is Common Lisp; and Common Lisp is a programming language.
ACL2!>(equal (app (app a b) c)
(app a (app b c))))
ACL2 Error in TOP-LEVEL: STATE is the only variable we permit to occur
freely in expressions to be evaluated, but C, B and A occur freely
in (EQUAL (APP (APP A B) C) (APP A (APP B C))). Embed symbols in (@
*) to access their global values.
This cryptic message means: you can't evaluate terms containing
unbound or free variables like a, b and c
above.
Actually, one free variable is permitted in top-level forms: the
variable state  , which denotes the current ACL2 state
and which is given very special treatment in this applicative
programming language. We do not discuss
, which denotes the current ACL2 state
and which is given very special treatment in this applicative
programming language. We do not discuss state here.
ACL2 provides a way for you to use state to save values of
computations at the top-level and refer to them later. See
assign  and @
and @  .
.


After collecting induction suggestions from these three terms
(app a b)the system notices that the first and last suggest the same decomposition of(app b c)
(app a (app b c))
a. So we are left with two ideas about how to induct:Decompose a as we would to unwind (app a b).
Decompose b as we would to unwind (app b c).


To find a plausible induction argument, the system studies the recursions exhibited by the terms in the conjecture.
Roughly speaking, a call of a recursive function ``suggests'' an induction if the argument position decomposed in recursion is occupied by a variable.
In this conjecture, three terms suggest inductions:
(app a b)The variable recursively decomposed is indicated in bold.(app b c)
(app a (app b c))


But ACL2 is more than a programming language.
Initialize x to 5 and let y be any legal value.
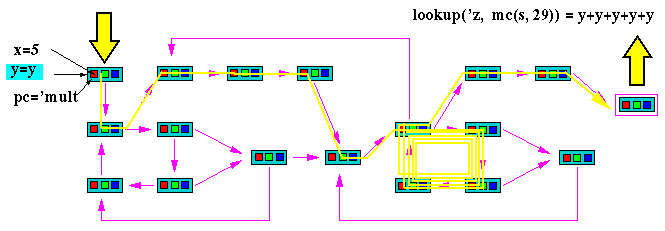
Because ACL2 is a mathematical language, we can simplify the expression
(lookup 'z (mc (s 'mult 5 y) 29))
and get (+ y y y y y). This is symbolic execution because not all of the parameters are known.
Here is what it looks like to submit the definition of app to ACL2:

ACL2 !>(defun app (x y)
(cond ((endp x) y)
(t (cons (car x)
(app (cdr x) y)))))
The admission of APP is trivial, using the relation E0-ORD-< (which
is known to be well-founded on the domain recognized by E0-ORDINALP)
and the measure (ACL2-COUNT X). We observe that the type of APP is
described by the theorem (OR (CONSP (APP X Y)) (EQUAL (APP X Y) Y)).
We used primitive type reasoning.
Summary
Form: ( DEFUN APP ...)
Rules: ((:FAKE-RUNE-FOR-TYPE-SET NIL))
Warnings: None
Time: 0.03 seconds (prove: 0.00, print: 0.00, other: 0.03)
APP

The text between the lines above is one interaction with the ACL2 command loop.
Above you see the user's input and how the system responds. This little example shows you what the syntax looks like and is a very typical successful interaction with the definitional principle.
Let's look at it a little more closely.

ACL2!>(let ((a '(1 2))
(b '(3 4))
(c '(5 6)))
(equal (app (app a b) c)
(app a (app b c))))
T

Observe that, for the particular a, b, and c above,
(app (app a b) c) returns the same thing as (app a (app b c)).
Perhaps app is associative. Of course, to be associative means
that the above property must hold for all values of a, b, and c,
not just the ones tested above.
Wouldn't it be cool if you could type
ACL2!>(equal (app (app a b) c)
(app a (app b c))))
and have ACL2 compute the value T? Well, you can't! If you try
it, you'll get an error message! The message says we can't evaluate
that form because it contains free variables, i.e., variables
not given values. Click here to see the
message.We cannot evaluate a form on an infinite number of cases. But we can prove that a form is a theorem and hence know that it will always evaluate to true.
This formula is the Base Case. It consists of two parts, a test identifying the non-inductive case and the conjecture to prove.
(IMPLIES (ENDP A) ; Test
(:P A B C)) ; Conjecture
When we prove this we can assume
* A is empty
and we have to prove the conjecture for A.



This completes the Flying Tour.
You may wish now to go back and revisit selected nodes of the Flying Tour so that you can explore some of the branches not on the Tour. You can do so via The Flight Plan. These branches mainly provide some background and motivational material, rather than details of ACL2.
If you would like to learn more about ACL2 itself, we recommend that you now take the walking Tour. You may do so by clicking on the Walking Tour icon below.
Thanks.
Matt Kaufmann and J Moore