

Next: Analysis of the
Up: The Model
Previous: The Model
In the Simplified Global ... section we discussed various simplified versions of the
overall model to be presented in this paper. There are some unanswered
questions raised by these models, and in particular, that of the stability
and flexibility of the system. In this section, we wish to present the more
complete model and discuss in general how it functions. Furthermore, we will
show how it possesses features able to give a broad range of responses to
inputs. Most specifically, we wish to show that parameter ranges can be varied
by internal and external factors.

Figure 2:
The wiring diagram of the main model of
the thalamus-NRT-cortex complex. Input  is sent to both the
thalamic relay cell
is sent to both the
thalamic relay cell  and the inhibitory interneuron
and the inhibitory interneuron  , which
itself feeds to
, which
itself feeds to 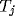 . Output from
. Output from  goes up to the corresponding
cortical cell
goes up to the corresponding
cortical cell  , which feeds back its output to
, which feeds back its output to  . Both the
axons
. Both the
axons 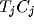 and
and  send axon collaterals to the corresponding
NRT cell
send axon collaterals to the corresponding
NRT cell  . There is axonal output from
. There is axonal output from  to
to  , as well
as collaterals to neighbouring NRT cells; there are also dendro-dendritic
synapses between the NRT cells.
, as well
as collaterals to neighbouring NRT cells; there are also dendro-dendritic
synapses between the NRT cells.
The basis of the model is best seen in terms of its wiring diagram in
Figure 2.
The model is an extension of that in Figure 1 by means of :
(i) addition of the cortical layer C,
(ii) addition of interneurons IN in thalamus,
(iii) extension of the input to IN cells as well as the T cells,
and NRT feedback solely taken to IN cells.
The latter conectivity is an approximation to the results of the analysis
of Steriade and colleagues [41], in which the effect of GABA on GABAergic
cells (from N cell feedback to IN cell) is claimed to be an order of magnitude
more effective than of GABA on excitatory cells. We note that the model may be
regarded as the framework for more extensive modelling with layered cortex
and NRT. However, at this stage, too much complexity would be introduced too
rapidly by such structural richness.
We now turn to the detail of the equations used to describe the
thalamus-NRT-cortex interacting system, whose general structure is
shown in Figure 2. Excitatory neurons are assumed to be at a coordinate
position  (using the same coordinate frame for thalamus, NRT and
cortex) on the thalamic and cortical sheets and to have membrane potentials
labelled
(using the same coordinate frame for thalamus, NRT and
cortex) on the thalamic and cortical sheets and to have membrane potentials
labelled  and
and  , and outputs
, and outputs  , (i=T and
C, respectively), where
, (i=T and
C, respectively), where  , with threshold
, with threshold  and temperature
and temperature  . Inhibitory
neurons in the thalamus and on the NRT (with the same coordinate positions)
have membrane potentials denoted by
. Inhibitory
neurons in the thalamus and on the NRT (with the same coordinate positions)
have membrane potentials denoted by 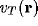 ,
,  , with
similar sigmoidal outputs
, with
similar sigmoidal outputs  ,
,  to the other neurons. Connection
weights from the j'th excitatory (inhibitory) neuron at
to the other neurons. Connection
weights from the j'th excitatory (inhibitory) neuron at  to the
i'th excitatory (inhibitory) neuron at
to the
i'th excitatory (inhibitory) neuron at  are denoted by
are denoted by
 ,
,  ,
,
 ,
, 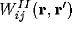 . The resulting
leaky integrator neurons (LINs) satisfy
. The resulting
leaky integrator neurons (LINs) satisfy




(where we are using the notation  ). We have rescaled
all the connection weights, and the input on the thalamic cells, so that the decay
constants
). We have rescaled
all the connection weights, and the input on the thalamic cells, so that the decay
constants  ,
,  drop out for stationary activity. Moreover the
dendro-dendritic contribution has yet to be included in (11), it being given
by the analysis of Taylor [43], as cited earlier, to be equal in the
linearised limit to
drop out for stationary activity. Moreover the
dendro-dendritic contribution has yet to be included in (11), it being given
by the analysis of Taylor [43], as cited earlier, to be equal in the
linearised limit to

A purely rectangular net with four neighbours at horizontal and
vertical distances  ,
,  (so
(so  ) gives,
in the continuum limit [43], the dendro-dendritic term is
) gives,
in the continuum limit [43], the dendro-dendritic term is
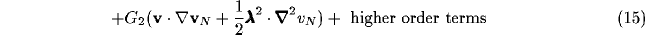
where  ,
,
 ,
,
 , and
, and
 is a negatively-valued constant in (15).
The equation (11) thus reduces to a negative Laplacian net, with a linear
derivative term proportional to
is a negatively-valued constant in (15).
The equation (11) thus reduces to a negative Laplacian net, with a linear
derivative term proportional to  . The inputs to the net depend,
however, in a non-linear manner on
. The inputs to the net depend,
however, in a non-linear manner on  as given by (12), (14), (15).
as given by (12), (14), (15).


Next: Analysis of the
Up: The Model
Previous: The Model

 is sent to both the
thalamic relay cell
is sent to both the
thalamic relay cell  and the inhibitory interneuron
and the inhibitory interneuron  , which
itself feeds to
, which
itself feeds to 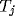 . Output from
. Output from  goes up to the corresponding
cortical cell
goes up to the corresponding
cortical cell  , which feeds back its output to
, which feeds back its output to  . Both the
axons
. Both the
axons 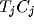 and
and  send axon collaterals to the corresponding
NRT cell
send axon collaterals to the corresponding
NRT cell  . There is axonal output from
. There is axonal output from  to
to  , as well
as collaterals to neighbouring NRT cells; there are also dendro-dendritic
synapses between the NRT cells.
, as well
as collaterals to neighbouring NRT cells; there are also dendro-dendritic
synapses between the NRT cells.
 (using the same coordinate frame for thalamus, NRT and
cortex) on the thalamic and cortical sheets and to have membrane potentials
labelled
(using the same coordinate frame for thalamus, NRT and
cortex) on the thalamic and cortical sheets and to have membrane potentials
labelled  and
and  , and outputs
, and outputs  , (i=T and
C, respectively), where
, (i=T and
C, respectively), where  , with threshold
, with threshold  and temperature
and temperature  . Inhibitory
neurons in the thalamus and on the NRT (with the same coordinate positions)
have membrane potentials denoted by
. Inhibitory
neurons in the thalamus and on the NRT (with the same coordinate positions)
have membrane potentials denoted by 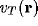 ,
,  , with
similar sigmoidal outputs
, with
similar sigmoidal outputs  ,
,  to the other neurons. Connection
weights from the j'th excitatory (inhibitory) neuron at
to the other neurons. Connection
weights from the j'th excitatory (inhibitory) neuron at  to the
i'th excitatory (inhibitory) neuron at
to the
i'th excitatory (inhibitory) neuron at  are denoted by
are denoted by
 ,
,  ,
,
 ,
, 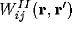 . The resulting
leaky integrator neurons (LINs) satisfy
. The resulting
leaky integrator neurons (LINs) satisfy




 ). We have rescaled
all the connection weights, and the input on the thalamic cells, so that the decay
constants
). We have rescaled
all the connection weights, and the input on the thalamic cells, so that the decay
constants  ,
,  drop out for stationary activity. Moreover the
dendro-dendritic contribution has yet to be included in (
drop out for stationary activity. Moreover the
dendro-dendritic contribution has yet to be included in (
 ,
,  (so
(so  ) gives,
in the continuum limit [
) gives,
in the continuum limit [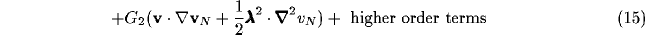
 ,
,
 ,
,
 , and
, and
 is a negatively-valued constant in (
is a negatively-valued constant in ( . The inputs to the net depend,
however, in a non-linear manner on
. The inputs to the net depend,
however, in a non-linear manner on  as given by (
as given by (