5 Performance

  In this section, we present performance data measures on a Cray T3E-600. While we have run the algorithms on many different machines, and many different numbers of nodes, the presented data was chosen since it is the most complete data for all different algorithms.

In our performance graphs in Fig. 5, we report millions of floating point operations per second (MFLOPS) per node attained by the algorithms. For the Cholesky, LU, and QR factorizations, we use the accepted operation counts of $\frac{1}{3} n^3$, $\frac{2}{3} n^3$, and $\frac{4}{3} n^3$, respectively. (Notice that we only measured performance for square matrices.) All computation was performed in 64-bit arithmetic. The LINPACK benchmark (essentially an LU factorization) on the same architecture and configuration attains close to 400 MFLOPS per node, but for a much larger problem (almost 20000x20000) than we measured.

   Figure 5: Performance of the various algorithms on a 16 processor configuration of the Cray T3E 600.

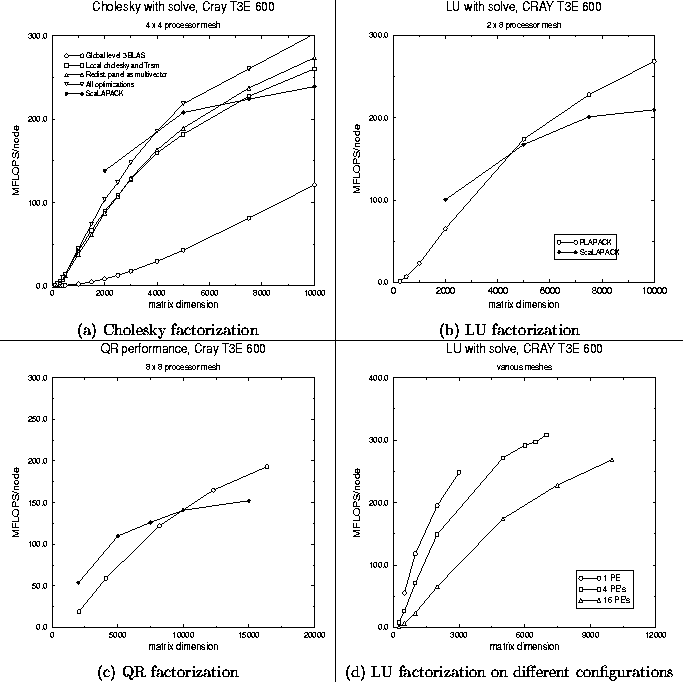
We compare performance of our implementations to performance attained by the routines with the same functionality provided by ScaLAPACK. The presented curves for ScaLAPACK were created with data from the ScaLAPACK Users' Guide [4]. While it is highly likely that that data was obtained with different versions of the OS, MPI, compilers, and BLAS, we did perform some measurements of ScaLAPACK routines on the same system on which our implementations were measured. The data in the ScaLAPACK Users' Guide was found to be representative of performance on our system.

In Fig. 5 (a), we present the performance of the various parallel Cholesky implementations presented in Section 2. The following table links the legend for the curves to the different implementations:

Recall that the basic implementation Global level 3 BLAS calls an unblocked parallel implementation of the Cholesky factorization, which incurs considerablein turn communication overhead. It is for this reason that performance is quite disappointing. Picking the block size so that this subproblem can be solved on a single node, and the corresponding triangular solve with multiple right-hand-sides on a single column of nodes, boosts performance to quite acceptable levels. Our new algorithm, which redistributes the panel to be factored before factoring, improves upon this performance somewhat. Final minor further optimizations, not described in this paper, boost the performance past 300 MFLOPS per node for problem sizes that fit our machine.

In Fig. 5 (b)-(c), we present only the ``new parallel algorithm'' versions of LU factorization and QR factorization. Performance behavior is quite similar to that observed by the Cholesky factorization. It is interesting to note that the performance of the QR factorization is considerably less than that of the Cholesky or LU factorization. This can be attributed to the fact that the QR factorization performs the operation $U = Y^T A_{B2}$ in addition to the rank-k update $A_{B2} \leftarrow A_{B2} + W U^T$.This, in turn, local on each node, calls a different case of the matrix-matrix multiplication kernel, which does not attain the same level of performance in the current implementation of the BLAS for the Cray T3E. We should note that the PLAPACK implementations use an algorithmic block size (nb_alg) of 128 and a distribution block size (nb_distr) of 64, while ScaLAPACK again uses blocking sizes of 32. Finally, in Fig. 5 (d), we present performance of the LU factorization on different numbers of nodes, which gives some indication of the scalability of the approach.

When comparing performance of PLAPACK and ScaLAPACK, it is clear that the PLAPACK overhead at this point does impose a penalty for small problem sizes. The algorithm used for Cholesky factorization by ScaLAPACK is roughly equivalent to the one marked Local Cholesky and Trsm in the graph. Even for the algorithm that is roughly equivalent to the ScaLAPACK implementation, PLAPACK outperforms ScaLAPACK for larger problem sizes. This is in part due to the fact that we use a larger algorithmic and distribution block size (64 vs. 32) for that algorithm. It is also due to the fact that we implemented the symmetric rank-k update (PLA_Syrk) differently from the ScaLAPACK equivalent routine (PSSYRK). We experimented with using an algorithmic and distribution block size of 64 for ScaLAPACK, but this did not improve performance. Unlike the more sophisticated algorithms implemented using PLAPACK, ScaLAPACK does not allow the algorithmic and distribution block size to differ.