ALAFF Unit ball

Skip to main content

\( \usepackage{array} \setlength{\oddsidemargin}{-0.0in} \setlength{\evensidemargin}{-0.0in} \setlength{\textheight}{8.75in} \setlength{\textwidth}{6.5in} \setlength{\topmargin}{-0.25in} \newcommand{\R}{\mathbb R} \newcommand{\Rm}{\mathbb R^m} \newcommand{\Rn}{\mathbb R^n} \newcommand{\Rnxn}{\mathbb R^{n \times n}} \newcommand{\Rmxn}{\mathbb R^{m \times n}} \newcommand{\Rmxm}{\mathbb R^{m \times m}} \newcommand{\Rmxk}{\mathbb R^{m \times k}} \newcommand{\Rkxn}{\mathbb R^{k \times n}} \newcommand{\C}{\mathbb C} \newcommand{\Cm}{\mathbb C^m} \newcommand{\Cmxm}{\mathbb C^{m \times m}} \newcommand{\Cnxn}{\mathbb C^{n \times n}} \newcommand{\Cmxn}{\mathbb C^{m \times n}} \newcommand{\Ckxk}{\mathbb C^{k \times k}} \newcommand{\Cn}{\mathbb C^n} \newcommand{\Ck}{\mathbb C^k} \newcommand{\Null}{{\cal N}} \newcommand{\Col}{{\cal C}} \newcommand{\Rowspace}{{\cal R}} \newcommand{\Span}{{\rm {Span}}} \newcommand{\rank}{{\rm rank}} \newcommand{\triu}{{\rm triu}} \newcommand{\tril}{{\rm tril}} \newcommand{\sign}{{\rm sign}} \newcommand{\FlaTwoByTwo}[4]{ \left( \begin{array}{c | c} #1 \amp #2 \\ \hline #3 \amp #4 \end{array} \right) } \newcommand{\FlaTwoByTwoSingleLine}[4]{ \left( \begin{array}{c c} #1 \amp #2 \\ #3 \amp #4 \end{array} \right) } \newcommand{\FlaTwoByTwoSingleLineNoPar}[4]{ \begin{array}{c c} #1 \amp #2 \\ #3 \amp #4 \end{array} } \newcommand{\FlaOneByTwo}[2]{ \left( \begin{array}{c | c} #1 \amp #2 \end{array} \right) } \newcommand{\FlaOneByTwoSingleLine}[2]{ \left( \begin{array}{c c} #1 \amp #2 \end{array} \right) } \newcommand{\FlaTwoByOne}[2]{ \left( \begin{array}{c} #1 \\ \hline #2 \end{array} \right) } \newcommand{\FlaTwoByOneSingleLine}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right) } \newcommand{\FlaThreeByOneB}[3]{ \left( \begin{array}{c} #1 \\ \hline #2 \\ #3 \end{array} \right) } \newcommand{\FlaThreeByOneT}[3]{ \left( \begin{array}{c} #1 \\ #2 \\ \hline #3 \end{array} \right) } \newcommand{\FlaOneByThreeR}[3]{ \left( \begin{array}{c | c c} #1 \amp #2 \amp #3 \end{array} \right) } \newcommand{\FlaOneByThreeL}[3]{ \left( \begin{array}{c c | c} #1 \amp #2 \amp #3 \end{array} \right) } \newcommand{\FlaThreeByThreeBR}[9]{ \left( \begin{array}{c | c c} #1 \amp #2 \amp #3 \\ \hline #4 \amp #5 \amp #6 \\ #7 \amp #8 \amp #9 \end{array} \right) } \newcommand{\FlaThreeByThreeTL}[9]{ \left( \begin{array}{c c | c} #1 \amp #2 \amp #3 \\ #4 \amp #5 \amp #6 \\ \hline #7 \amp #8 \amp #9 \end{array} \right) } \newcommand{\diag}[1]{{\rm diag}( #1 )} \newcommand{\URt}{{\sc HQR}} \newcommand{\FlaAlgorithm}{ \begin{array}{|l|} \hline \routinename \\ \hline \partitionings \\ ~~~ \begin{array}{l} \partitionsizes \end{array} \\ {\bf \color{blue} {while}~} \guard \\ ~~~ \begin{array}{l} \repartitionings \end{array} \\ ~~~ \color{red} { \begin{array}{l} \hline \color{black} {\update} \\ \hline \end{array}} \\ ~~~ \begin{array}{l} \moveboundaries \end{array} \\ {\bf \color{blue} {endwhile}} \\ \hline \end{array} } \newcommand{\FlaAlgorithmWithInit}{ \begin{array}{|l|} \hline \routinename \\ \hline \initialize \\ \partitionings \\ ~~~ \begin{array}{l} \partitionsizes \end{array} \\ {\bf \color{blue} {while}~} \guard \\ ~~~ \begin{array}{l} \repartitionings \end{array} \\ ~~~ \color{red} { \begin{array}{l} \hline \color{black} {\update} \\ \hline \end{array}} \\ ~~~ \begin{array}{l} \moveboundaries \end{array} \\ {\bf \color{blue} {endwhile}} \\ \hline \end{array} } \newcommand{\FlaBlkAlgorithm}{ \begin{array}{|l|} \hline \routinename \\ \hline \partitionings \\ ~~~ \begin{array}{l} \partitionsizes \end{array} \\ {\bf \color{blue} {while}~} \guard \\ ~~~ {\bf choose~block~size~} \blocksize \\ ~~~ \begin{array}{l} \repartitionings \end{array} \\ ~~~ ~~~ \repartitionsizes \\ ~~~ \color{red} { \begin{array}{l} \hline \color{black} {\update} \\ \hline \end{array}} \\ ~~~ \begin{array}{l} \moveboundaries \end{array} \\ {\bf \color{blue} {endwhile}} \\ \hline \end{array} } \newcommand{\complexone}{ \begin{array}{|c|}\hline \!\pm\! \\ \hline \end{array}~ } \newcommand{\HQR}{{\rm HQR}} \newcommand{\QR}{{\rm QR}} \newcommand{\st}{{\rm \ s.t. }} \newcommand{\QRQ}{{\rm {\normalsize \bf Q}{\rm \tiny R}}} \newcommand{\QRR}{{\rm {\rm \tiny Q}{\bf \normalsize R}}} \newcommand{\deltaalpha}{\delta\!\alpha} \newcommand{\deltax}{\delta\!x} \newcommand{\deltay}{\delta\!y} \newcommand{\deltaz}{\delta\!z} \newcommand{\deltaw}{\delta\!w} \newcommand{\DeltaA}{\delta\!\!A} \newcommand{\meps}{\epsilon_{\rm mach}} \newcommand{\fl}[1]{{\rm fl( #1 )}} \newcommand{\becomes}{:=} \newcommand{\defrowvector}[2]{ \left(#1_0, #1_1, \ldots, #1_{#2-1}\right) } \newcommand{\tr}[1]{{#1}^T} \newcommand{\LUpiv}[1]{{\rm LU}(#1)} \newcommand{\maxi}{{\rm maxi}} \newcommand{\Chol}[1]{{\rm Chol}( #1 )} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Subsection 1.2.5 Unit ball

In 3-dimensional space, the notion of the unit ball is intuitive: the set of all points that are a (Euclidean) distance of one from the origin. Vectors have no position and can have more than three components. Still the unit ball for the 2-norm is a straight forward extension to the set of all vectors with length (2-norm) one. More generally, the unit ball for any norm can be defined:

Definition 1.2.5.1. Unit ball.

Given norm \(\| \cdot \| : \Cm \rightarrow \mathbb R \text{,}\) the unit ball with respect to \(\| \cdot \|\) is the set \(\{ x ~\vert ~ \| x \| = 1 \} \) (the set of all vectors with norm equal to one). We will use \(\| x \| = 1 \) as shorthand for \(\{ x ~\vert ~ \| x \| = 1 \} \text{.}\)

Homework 1.2.5.1.

Although vectors have no position, it is convenient to visualize a vector \(x \in \R^2 \) by the point in the plane to which it extends when rooted at the origin. For example, the vector \(x = \left( \begin{array}{c} 2 \\ 1 \end{array} \right) \) can be so visualized with the point \(( 2, 1 ) \text{.}\) With this in mind, match the pictures on the right corresponding to the sets on the left:

(a) \(\| x \|_2 = 1 \text{.}\)

(1)

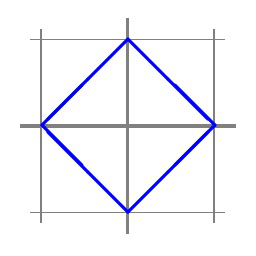
(b) \(\| x \|_1 = 1 \text{.}\)

(2)

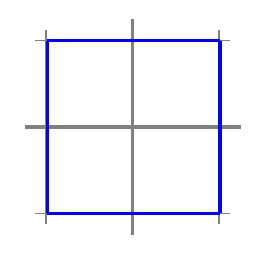
(c) \(\| x \|_\infty = 1 \text{.}\)

(3)

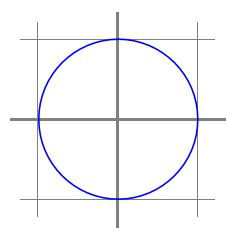
(a) \(\| x \|_2 = 1 \text{.}\)

(3)

(b) \(\| x \|_1 = 1 \text{.}\)

(1)

(c) \(\| x \|_\infty = 1 \text{.}\)

(2)