Skip to main content

Unit 1.1.1 Launch

Homework 1.1.1.1.

Compute \(\left(\begin{array}{rrr} 1 \amp -2 \amp 2\\ 1 \amp 1 \amp 3\\ -2 \amp 2 \amp 1 \end{array}\right) \left(\begin{array}{rr} -2 \amp 1\\ 1 \amp 3\\ -1 \amp 2 \end{array}\right) + \left(\begin{array}{rr} 1 \amp 0\\ -1 \amp 2\\ -2 \amp 1 \end{array}\right) = \)

Answer

\(\left(\begin{array}{rrr} 1 \amp -2 \amp 2\\ 1 \amp 1 \amp 3\\ -2 \amp 2 \amp 1 \end{array}\right) \left(\begin{array}{rr} -2 \amp 1\\ 1 \amp 3\\ -1 \amp 2 \end{array}\right) + \left(\begin{array}{rr} 1 \amp 0\\ -1 \amp 2\\ -2 \amp 1 \end{array}\right) = \left(\begin{array}{rr} -5 \amp -1\\ -5 \amp 12\\ 3 \amp 7 \end{array}\right)\)

Let us explicitly define some notation that we will use to discuss matrix-matrix multiplication more abstractly.

Let \(A \text{,}\) \(B \text{,}\) and \(C \) be \(m \times k \text{,}\) \(k \times n \text{,}\) and \(m \times n \) matrices, respectively. We can expose their individual entries as

\begin{equation*} A = \left(\begin{array}{c c c c} \alpha_{0,0} \amp \alpha_{0,1} \amp \cdots \amp \alpha_{0,k-1} \\ \alpha_{1,0} \amp \alpha_{1,1} \amp \cdots \amp \alpha_{1,k-1} \\ \vdots \amp \vdots \amp \amp \vdots \\ \alpha_{m-1,0} \amp \alpha_{m-1,1} \amp \cdots \amp \alpha_{m-1,k-1} \end{array} \right), B = \left(\begin{array}{c c c c} \beta_{0,0} \amp \beta_{0,1} \amp \cdots \amp \beta_{0,n-1} \\ \beta_{1,0} \amp \beta_{1,1} \amp \cdots \amp \beta_{1,n-1} \\ \vdots \amp \vdots \amp \amp \vdots \\ \beta_{k-1,0} \amp \beta_{k-1,1} \amp \cdots \amp \beta_{k-1,n-1} \end{array} \right), \end{equation*}

and

\begin{equation*} C = \left(\begin{array}{c c c c} \gamma_{0,0} \amp \gamma_{0,1} \amp \cdots \amp \gamma_{0,n-1} \\ \gamma_{1,0} \amp \gamma_{1,1} \amp \cdots \amp \gamma_{1,n-1} \\ \vdots \amp \vdots \amp \amp \vdots \\ \gamma_{m-1,0} \amp \gamma_{m-1,1} \amp \cdots \amp \gamma_{m-1,n-1} \end{array} \right). \end{equation*}

The computation \(C := A B + C \text{,}\) which adds the result of matrix-matrix multiplication \(A B \) to a matrix \(C \text{,}\) is defined as

\begin{equation} \gamma_{i,j} := \sum_{p=0}^{k-1} \alpha_{i,p} \beta_{p,j} + \gamma_{i,j}\label{week1-eqn-gamma}\tag{1.1.1} \end{equation}

for all \(0 \leq i \lt m \) and \(0 \leq j \lt n \text{.}\) Why we add to \(C \) will become clear later. This leads to the following pseudo-code for computing \(C := A B + C \text{:}\)

\begin{equation*} \begin{array}{l} {\bf for~} i := 0, \ldots , m-1 \\ ~~~ {\bf for~} j := 0, \ldots , n-1 \\ ~~~~~~ {\bf for~} p := 0, \ldots , k-1 \\ ~~~~~~~~~ \gamma_{i,j} := \alpha_{i,p} \beta_{p,j} + \gamma_{i,j} \\ ~~~~~~{\bf end} \\ ~~~{\bf end} \\ {\bf end} \end{array} \end{equation*}

The outer two loops visit each element of \(C \text{,}\) and the inner loop updates \(\gamma_{i,j} \) with (1.1.1).

#define alpha( i,j ) A[ (j)*ldA + i ]   // map alpha( i,j ) to array A 
#define beta( i,j )  B[ (j)*ldB + i ]   // map beta( i,j )  to array B
#define gamma( i,j ) C[ (j)*ldC + i ]   // map gamma( i,j ) to array C

void MyGemm( int m, int n, int k, double *A, int ldA,
	     double *B, int ldB, double *C, int ldC )
{
  for ( int i=0; i<m; i++ )
    for ( int j=0; j<n; j++ )
      for ( int p=0; p<k; p++ )
        gamma( i,j ) += alpha( i,p ) * beta( p,j );
}

Figure 1.1.1. Implementation, in the C programming language, of the IJP ordering for computing matrix-matrix multiplication.

On Robert's laptop, Homework 1.1.1.2 yields the graph

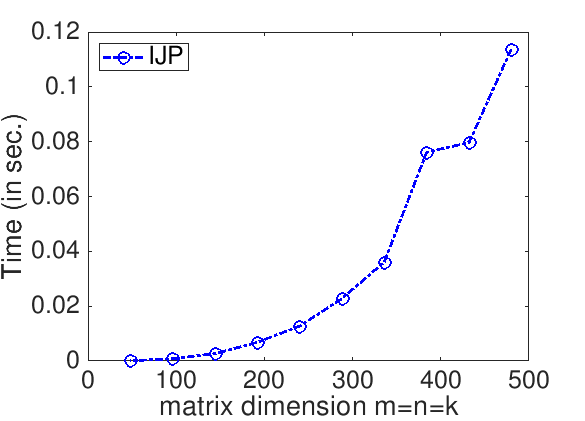
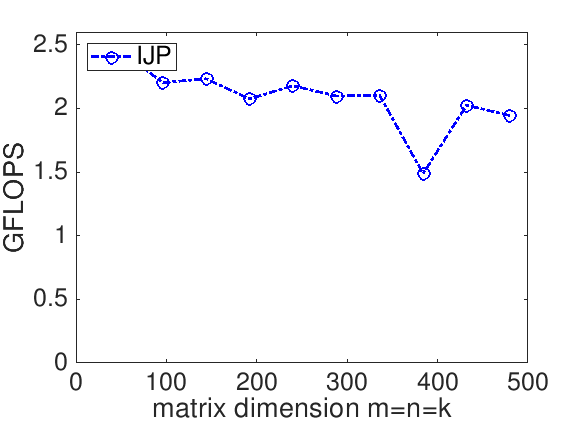
as the curve labeled with IJP. The time, in seconds, required to compute matrix-matrix multiplication as a function of the matrix size is plotted, where \(m = n = k \) (each matrix is square). The "dips" in the time required to complete can be attributed to a number of factors, including that other processes that are executing on the same processor may be disrupting the computation. One should not be too concerned about those.

The performance of a matrix-matrix multiplication implementation is measured in billions of floating point operations (flops) per second (GFLOPS). The idea is that we know that it takes \(2 m n k \) flops to compute \(C := A B + C \) where \(C \) is \(m \times n \text{,}\) \(A\) is \(m \times k \text{,}\) and \(B \) is \(k \times n \text{.}\) If we measure the time it takes to complete the computation, \(T( m, n, k ) \text{,}\) then the rate at which we compute is given by

\begin{equation*} \frac{2 m n k}{T(m,n,k)} \times 10^{-9} {\rm ~GFLOPS}. \end{equation*}

For our implementation and the reference implementation, this yields

Again, don't worry too much about the dips in the curves. If we controlled the environment in which we performed the experiments, (for example, by making sure few other programs are running at the time of the experiments) these would largely disappear.

Remark 1.1.2.

The Gemm in the name of the routine stands for General Matrix-Matrix multiplication. Gemm is an acronym that is widely used in scientific computing, with roots in the Basic Linear Algebra Subprograms (BLAS) discussed in the enrichment in Unit 1.5.1.

login