The simulation model we investigated is illustrated in Figure 2. It is essentially one-dimensional, which corresponds to lines of thalamic, NRT and cortical neurons. In future work, it is intended to extend the simulation work to the more realistic case of two-dimensional sheets of these neurons.
A simplified version of Figure 2 is presented in Figure 5. It is useful for simulation purposes to think of the boxed subsystem in Figure 5 as a single module that can be linearly replicated (with bidirectional lateral links among the NRT units). This allows the size of the simulation to be scaled to suit the available computing power.
Within each module, we have inter-unit signal flow as specified by the arrow-tipped curves. Every tip labelled with a `+' signifies an excitatory signal, while every `-' corresponds to an inhibitory signal. Within every module, the time evolution of each neural unit's voltage is determined by the solution of equations (10)--(14). Within a computing context, of course, a discretised version of these equations has to be integrated over some suitable small time step (we used the Runge-Kutta fourth-order integration routine). Such a scheme entails in practice that we replace the hard-limiting non-linearity by a smooth analytical function. We adopted the following form, as used by La Berge et al. [33]:
where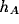 
is a scaling parameter, 
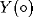is the step function,
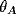is the threshold for unit A and 
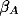is its inverse
temperature.
In order to proceed with the simulations, it was found necessary to obtain limits on
the ranges of the large number of parameters involved. To obtain an idea of what
constitutes `good' parameter ranges, consider the equations (10)--(14) in the static
limit (obtained by setting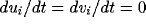 
, or, equivalently, by allowing the
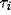's, i=T, N, C to go to zero):
Note that in these equations, we have taken the full non-linearity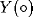 
for the function in (21). To distinguish between zero and finite external
inputs, we define further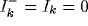 
and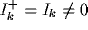 
.
In order to set up the subsystem so that we can achieve global control, we
require that units T,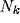 
and C be switched `off' whenever unit I is
`on' in the case of zero external input, and vice versa in the case
of finite external input
. Looking at (25) separately for the case when
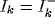and 
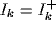, it is easy to show that the thresholds of each
of the units have to lie in the ranges
