Section 2 What will I learn in this course?
This course discusses discrete mathematics, the part of mathematics devoted to the study of distinct or unconnected elements. Discrete mathematics provides the mathematical foundations for many computer science classes, including data structures, algorithms, database theory, automata theory, formal languages, compilers, security and operating systems.
Subsection 2.1 Learning Goals
Develop logical thinking to draw conclusions based on chains of reasoning
Present coherent and mathematically accurate arguments.
Apply reasoning skills to various discrete objects used to analyze programs.
Subsection 2.2 Textbook
Kenneth H. Rosen. Discrete Mathematics and its Applications, 8th Edition, McGraw Hill.
This textbook is not required, meaning there will be no reading assigned or problems assigned from the textbook. However, the textbook may serve as an additional resourse.
Subsection 2.3 Topics
Proposition Logic; Predicates; Quantifiers; Encode statements into predicates with quantifiers; Boolean formulas; the notion of Satisfiability.
Basic Proof Techniques–Direct Proof; Proof by Contradiction; Simple Examples; Refresher on summation notation.
Induction and Invariants–Basic proofs by induction; Proving simple invariants
Graph Theory–Graph Coloring and applications; Trees; Planarity; Proving simple graph properties using induction
Sets and Functions–Definitions, Relations; Injections, Surjections, and Bijections; Infinite sets; uncountability
Recurrences–Recurrence relations; Solving Linear recurrences
Big-O and Intro to Algorithms–Growth of common functions; Big-O and Big-Omega; Master Theorem
Subsection 2.4 Detailed Calendar
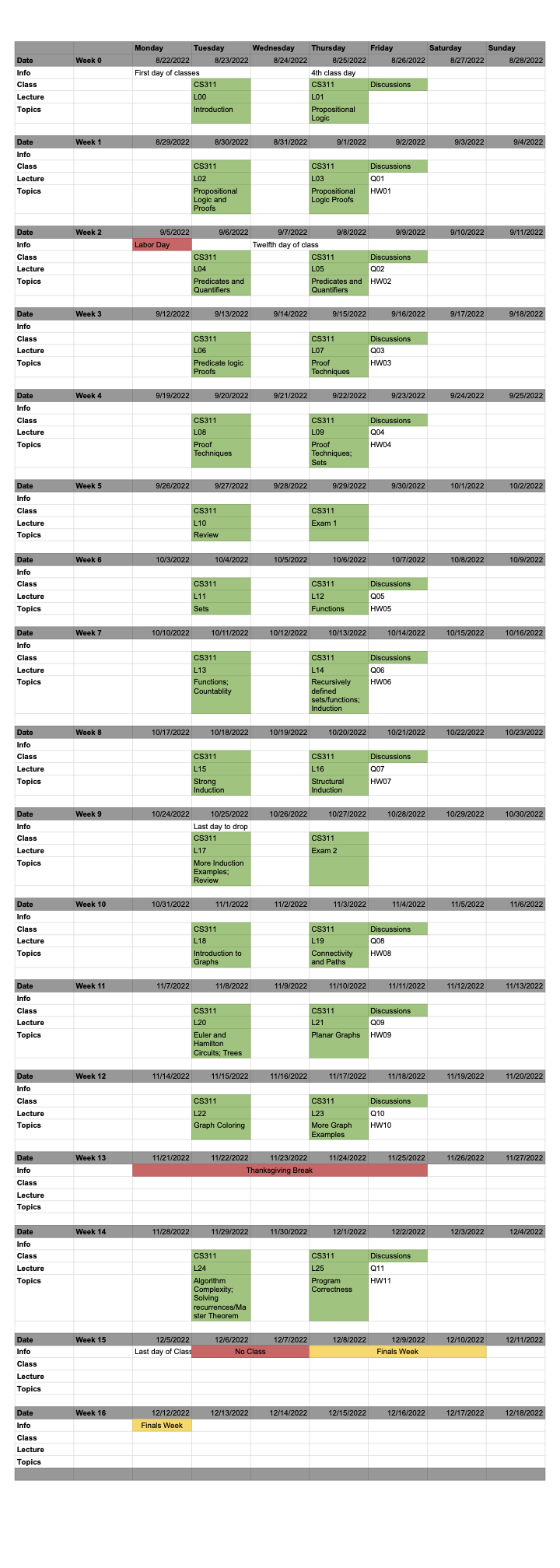
hereFigure 2.1 shows the schedule for the semester. Here you can find the dates of all the lectures, homeworks, quizzes, and exams. This schedule is subject to change during the semester. However, Exam dates are final.
