My research has focused primarily on physical simulation and geometry processing.
Click the project titles or thumbnails to go to the project page/paper.
Click the project titles or thumbnails to go to the project page/paper.
|
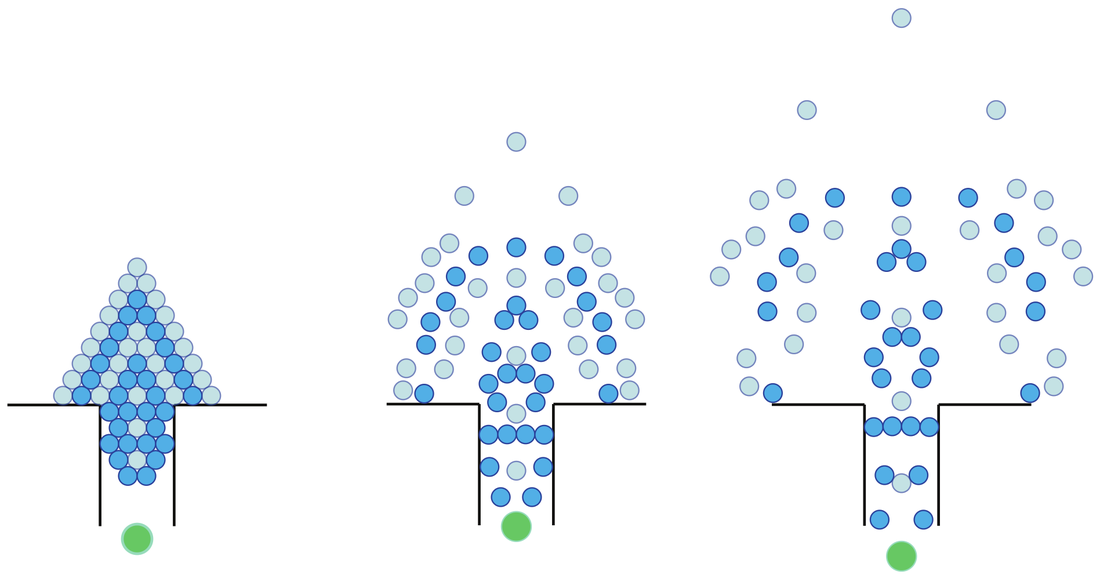
C-Space Tunnel Discovery for Puzzle Path Planning
Xinya Zhang, Robert Belfer, Paul G. Kry, Etienne Vouga SIGGRAPH, 2020. Rigid body disentanglement puzzles are challenging for both humans and motion planning algorithms because their solutions involve tricky twisting and sliding moves that correspond to navigating through narrow tunnels in the puzzle’s configuration space (C-space). We propose a tunnel-discovery and planning strategy for solving these puzzles. First, we locate important features on the pieces using geometric heuristics and machine learning, and then match pairs of these features to discover collision free states in the puzzle’s C-space that lie within the narrow tunnels. Second, we propose a Rapidly-exploring Dense Tree (RDT) motion planner variant that builds tunnel escape roadmaps and then connects these roadmaps into a solution path connecting start and goal states. We evaluate our approach on a variety of challenging disentanglement puzzles and provide extensive baseline comparisons with other motion planning techniques. |
|
Octahedral Frames for Feature-Aligned Cross Fields
Paul Zhang, Josh Vekhter, Edward Chien, David Bommes, Etienne Vouga, Justin Solomon ACM Transactions on Graphics, 2020. We present a method for designing smooth cross fields on surfaces that automatically align to sharp features of an underlying geometry. Our approach introduces a novel class of energies based on a representation of cross fields in the spherical harmonic basis. We provide theoretical analysis of these energies in the smooth setting, showing that they penalize deviations from surface creases while otherwise promoting intrinsically smooth fields. We demonstrate the applicability of our method to quad meshing and include an extensive benchmark comparing our fields to other automatic approaches for generating feature-aligned cross fields on triangle meshes. |
|
Deep Generative Modeling for Scene Synthesis via Hybrid Representations
Zaiwei Zhang, Zhenpei Yang, Chongyang Ma, Linjie Luo, Alexander Huth, Etienne Vouga, Qixing Huang ACM Transactions on Graphics, 2019. We present a deep generative scene modeling technique for indoor environments. Our goal is to train a generative model using a feed-forward neural network that maps a prior distribution (e.g., a normal distribution) to the distribution of primary objects in indoor scenes. We introduce a 3D object arrangement representation that models the locations and orientations of objects, based on their size and shape attributes. Moreover, our scene representation is applicable for 3D objects with different multiplicities (repetition counts), selected from a database. We show a principled way to train this model by combining discriminator losses for both a 3D object arrangement representation and a 2D image-based representation. We demonstrate the effectiveness of our scene representation and the deep learning method on benchmark datasets. We also show the applications of this generative model in scene interpolation and scene completion. |
|
Weaving Geodesic Foliations
Josh Vekhter, Jiacheng Zhuo, Luisa F. Gil Fandino, Qixing Huang, Etienne Vouga SIGGRAPH, 2019. We study discrete geodesic foliations of surfaces---foliations whose leaves are all approximately geodesic curves---and develop several new variational algorithms for computing such foliations. Our key insight is a relaxation of vector field integrability in the discrete setting, which allows us to optimize for curl-free unit vector fields that remain well-defined near singularities and robustly recover a scalar function whose gradient is well aligned to these fields. We then connect the physics governing surfaces woven out of thin ribbons to the geometry of geodesic foliations, and present a design and fabrication pipeline for approximating surfaces of arbitrary geometry and topology by triaxially-woven structures, where the ribbon layout is determined by a geodesic foliation on a sixfold branched cover of the input surface. We validate the effectiveness of our pipeline on a variety of simulated and fabricated woven designs, including an example for readers to try at home. |
|
Localized Patterns in Crushed Conical Shells
Omer Gottesman, Etienne Vouga, Shmuel M. Rubinstein, L. Mahadevan Europhysics Letters, 2018. We use experiments and numerical simulations to study the rapid buckling of thin-walled cones as they impact a solid surface at high velocities. The buildup of air pressure inside the cone localizes the deformations to the impacting interface with the solid surface, leading to the hierarchical formation of an ordered pattern of small rhomboidal cells. In contrast, when the inner air pressure is not allowed to develop, the ordered pattern is destabilized and the cone collapses in a highly disordered state on long length scales. Numerical simulations confirm that the transition between ordered and disordered crumpling is governed by the competition between the elastic deformation energy of the shells and the work required to pressurize the air. Our results show how dynamic stabilization via tensioning suppresses long wavelength subcritical instabilities in shells and leads to the localization and propagation of short wavelength patterns. |
|
Fluid Brush
Sarah Abraham, Etienne Vouga, Donald Fussell Expressive, 2018. Digital media allows artists to create a wealth of visually-interesting effects that are impossible in traditional media. This includes temporal effects, such as cinemagraph animations, and expressive fluid effects. Yet these flexible and novel media often require highly technical expertise, which is outside a traditional artist’s skill with paintbrush or pen. Fluid Brush acts a form of novel, digital media,which retains the brush-based interactions of traditional media,while expressing the movement of turbulent and laminar flow. Asa digital media controlled through a non-technical interface, Fluid Brush allows for a novel form of painting that makes fluid effects accessible to novice users and traditional artists. To provide an informal demonstration of the medium’s effects, applications, and accessibility, we asked designers, traditional artists, and digital artists to experiment with Fluid Brush. They produced a variety of works reflective of their artistic interests and backgrounds. |
|
Physical Simulation of Environmentally Induced Thin Shell Deformation
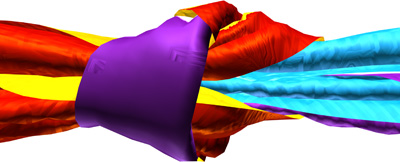
Hsiao-Yu Chen, Arnav Sastry, Wim M. van Rees, Etienne Vouga SIGGRAPH, 2018. We present a physically accurate low-order elastic shell model that incorporates active material response to dynamically changing stimuli such as heat, moisture, and growth. Our continuous formulation of the geometrically non-linear elastic energy derives from the principles of differential geometry, and as such naturally incorporates shell thickness, non-zero rest curvature, and physical material properties. By modeling the environmental stimulus as local, dynamic changes in the rest metric of the material, we are able to solve for the corresponding shape changes by integrating the equations of motions given this non-Euclidean rest state. We present models for differential growth and shrinking due to moisture and temperature gradients along and across the surface, and incorporate anisotropic growth by defining an intrinsic machine direction within the material. Comparisons with experiments and volumetric finite elements show that our simulations achieve excellent qualitative and quantitative agreement. By combining the reduced-order shell theory with appropriate physical models, our approach accurately captures all the physical phenomena while avoiding expensive volumetric discretization of the shell volume Some related source code is available here. |
|
Functional Generative Design: An Evolutionary Approach to 3D-Printing
Cem C. Tutum, Supawit Chockchowwat, Etienne Vouga, Risto Miikkulainen GECCO, 2018. Consumer-grade printers are widely available, but their ability to print complex objects is limited. Therefore, new designs need to be discovered that serve the same function, but are printable. A representative such problem is to produce a working, reliable mechanical spring. The proposed methodology for discovering solutions to this problem consists of three components: First, an effective search space is learned through a variational autoencoder (VAE); second, a surrogate model for functional designs is built; and third, a genetic algorithm is used to simultaneously update the hyperparameters of the surrogate and to optimize the designs using the updated surrogate. Using a car-launcher mechanism as a test domain, spring designs were 3D-printed and evaluated to update the surrogate model. Two experiments were then performed: First, the initial set of designs for the surrogate-based optimizer was selected randomly from the training set that was used for training the VAE model, which resulted in an exploitative search behavior. On the other hand, in the second experiment, the initial set was composed of more uniformly selected designs from the same training set and a more explorative search behavior was observed. Both of the experiments showed that the methodology generates interesting, successful, and reliable spring geometries robust to the noise inherent in the 3D printing process. The methodology can be generalized to other functional design problems, thus making consumer-grade 3D printing more versatile. |
|
Growth Patterns for Shape-shifting Elastic Bilayers
Wim M. van Rees, Etienne Vouga, and L. Mahadevan PNAS, 2017. Inspired by the differential-growth-driven morphogenesis of leaves, flowers, and other tissues, there is increasing interest in artificial analogs of these shape-shifting thin sheets made of active materials that respond to environmental stimuli such as heat, light, and humidity. But how can we determine the growth patterns to achieve a given shape from another shape? We solve this geometric inverse problem of determining the growth factors and directions (the metric tensors) for a given isotropic elastic bilayer to grow into a target shape by posing and solving an elastic energy minimization problem. A mathematical equivalence between bilayers and curved monolayers simplifies the inverse problem considerably by providing algebraic expressions for the growth metric tensors in terms of those of the final shape. This approach also allows us to prove that we can grow any target surface from any reference surface using orthotropically growing bilayers. We demonstrate this by numerically simulating the growth of a flat sheet into a face, a cylindrical sheet into a flower, and a flat sheet into a complex canyon-like structure |
|
Evolutionary Decomposition for 3D Printing
Eric A. Yu, Jim Yeom, Cem C. Tutum, Etienne Vouga, Risto Miikkulainen GECCO (Best Paper Award), 2017. Capabilities of extrusion-based 3D-printers have progressed significantly, but complex forms are still challenging to print. One major problem is overhanging surfaces. These surfaces require extra support structure to be printed, wasting material and time. Furthermore, delicate parts of the object can be damaged when these structures are removed. One potential solution is to print the object in parts, but decomposition is difficult. This paper proposes an evolutionary approach for determining optimal object decompositions for 3D printing. Two alternative methods, with different complementary strengths, are tested: Multi-objective Genetic Algorithm (MOGA) and Covariance Matrix Adaptation Evolution Strategy (CMA-ES). MOGA is able to evolve a set of decompositions at variable complexity, i.e. number of pieces, whereas CMA-ES is able to find a limited number of comparable decompositions with significantly less computational time. |
|
All's Well That Ends Well: Guaranteed Resolution of Simultaneous Rigid Body Impact
Etienne Vouga, Breannan Smith, Danny M. Kaufman, Rasmus Tamstorf, Eitan Grinspun SIGGRAPH (ACM Transactions on Graphics), 2017 Iterative algorithms are frequently used to resolve simultaneous impacts between rigid bodies in physical simulations. However, these algorithms lack formal guarantees of termination, which is sometimes viewed as potentially dangerous, so failsafes are used in practical codes to prevent infinite loops. We show such steps are unnecessary. In particular, we study the broad class of such algorithms that are conservative and satisfy a minimal set of physical correctness properties, and which encompasses recent methods like Generalized Reflections as well as pairwise schemes. We fully characterize finite termination of these algorithms. The only possible failure cases can be detected, and we describe a procedure for modifying the algorithms to provably ensure termination. We also describe modifications necessary to guarantee termination in the presence of numerical error due to the use of floating-point arithmetic. Finally, we discuss the challenges dissipation introduce for finite termination, and describe how dissipation models can be incorporated while retaining the termination guarantee. |
|
On the Incompressibility of Cylindrical Origami Patterns
Friedrich Bös, Max Wardetzky, Etienne Vouga, and Omer Gottesman Journal of Mechanical Design, 2016 The art and science of folding intricate three-dimensional structures out of paper has occupied artists, designers, engineers, and mathematicians for decades, culminating in the design of deployable structures and mechanical metamaterials. Here we investigate the axial compressibility of origami cylinders, i.e., cylindrical structures folded from rectangular sheets of paper. We prove, using geometric arguments, that a general fold pattern only allows for a finite number of isometric cylindrical embeddings. Therefore, compressibility of such structures requires either stretching the material or deforming the folds. Our result considerably restricts the space of constructions that must be searched when designing new types of origami-based rigid-foldable deployable structures and metamaterials. |
|
Programming Curvature Using Origami Tessellations
Levi H. Dudte, Etienne Vouga, Tomohiro Tachi, and L. Mahadevan Nature Materials, 2016 Origami describes rules for creating folded structures from patterns on a flat sheet, but does not prescribe how patterns can be designed to fit target shapes. Here, starting from the simplest periodic origami pattern that yields one-degree-of-freedom collapsible structures—we show that scale-independent elementary geometric constructions and constrained optimization algorithms can be used to determine spatially modulated patterns that yield approximations to given surfaces of constant or varying curvature. Paper models confirm the feasibility of our calculations. We also assess the difficulty of realizing these geometric structures by quantifying the energetic barrier that separates the metastable flat and folded states. Moreover, we characterize the trade-off between the accuracy to which the pattern conforms to the target surface, and the effort associated with creating finer folds. Our approach enables the tailoring of origami patterns to drape complex surfaces independent of absolute scale, as well as the quantification of the energetic and material cost of doing so. |
|
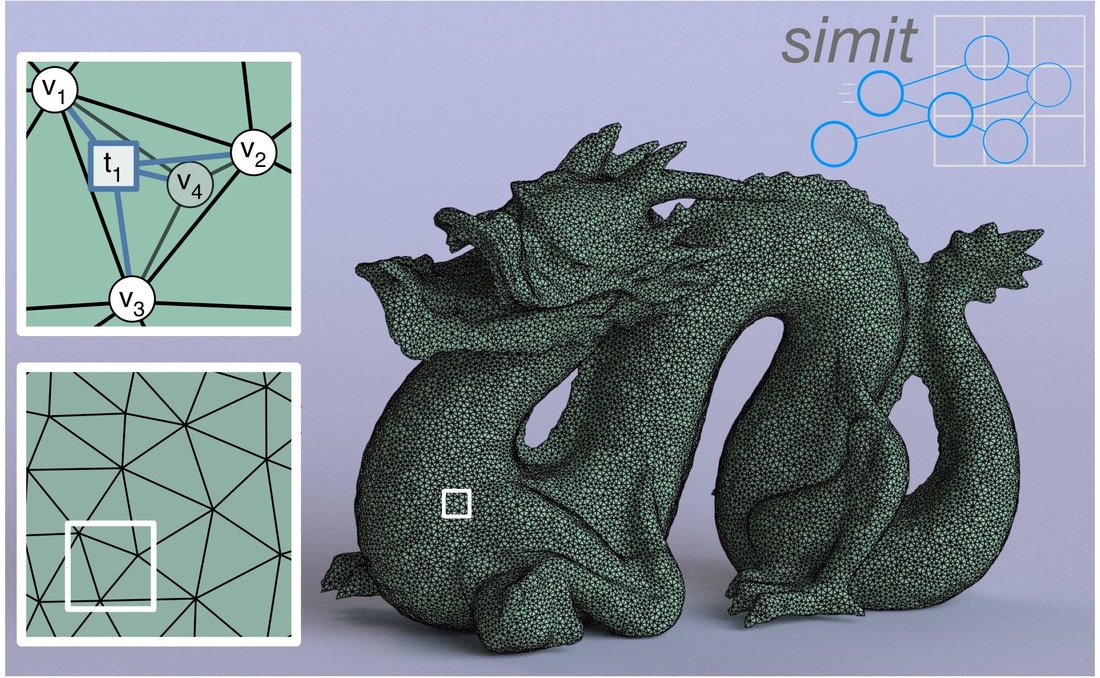
Simit: A Language for Physical Simulation
Fredrik Kjolstad, Shoaib Kamil, Jonathan Ragan-Kelley, David I. W. Levin, Shinjiro Sueda, Desai Chen, Etienne Vouga, Danny M. Kaufman, Gurtej Kanwar, Wojciech Matusik, and Saman Amarasinghe ACM Transactions on Graphics, 2016 With existing programming tools, writing high-performance simulation code is labor intensive and requires sacrificing readability and portability. The alternative is to prototype simulations in a high-level language like Matlab, thereby sacrificing performance. The Matlab programming model naturally describes the behavior of an entire physical system using the language of linear algebra. However, simulations also manipulate individual geometric elements, which are best represented using linked data structures like meshes. Translating between the linked data structures and linear algebra comes at significant cost, both to the programmer and to the machine. High-performance implementations avoid the cost by rephrasing the computation in terms of linked or index data structures, leaving the code complicated and monolithic, often increasing its size by an order of magnitude. In this article, we present Simit, a new language for physical simulations that lets the programmer view the system both as a linked data structure in the form of a hypergraph and as a set of global vectors, matrices, and tensors depending on what is convenient at any given time. Simit provides a novel assembly construct that makes it conceptually easy and computationally efficient to move between the two abstractions. Using the information provided by the assembly construct, the compiler generates efficient in-place computation on the graph. We demonstrate that Simit is easy to use: a Simit program is typically shorter than a Matlab program; that it is high performance: a Simit program running sequentially on a CPU performs comparably to hand-optimized simulations; and that it is portable: Simit programs can be compiled for GPUs with no change to the program, delivering 4 to 20× speedups over our optimized CPU code. |
|
Capturing Dynamic Textured Surfaces of Moving Targets
Ruizhe Wang, Lingyu Wei, Etienne Vouga, Qixing Huang, Duygu Ceylan, Gerard Medioni, and Hao Li ECCV (spotlight), 2016 We present an end-to-end system for reconstructing complete watertight and textured models of moving subjects such as clothed humans and animals, using only three or four handheld sensors. The heart of our framework is a new pairwise registration algorithm that minimizes, using a particle swarm strategy, an alignment error metric based on mutual visibility and occlusion. We show that this algorithm reliably registers partial scans with as little as 15% overlap without requiring any initial correspondences, and outperforms alternative global registration algorithms. This registration algorithm allows us to reconstruct moving subjects from free-viewpoint video produced by consumer-grade sensors, without extensive sensor calibration, constrained capture volume, expensive arrays of cameras, or templates of the subject geometry. |
|
Dense Human Body Correspondences Using Convolutional Networks
Lingyu Wei, Qixing Huang, Duygu Ceylan, Etienne Vouga, and Hao Li CVPR (oral), 2016 We propose a deep learning approach for finding dense correspondences between 3D scans of people. Our method requires only partial geometric information in the form of two depth maps or partial reconstructed surfaces, works for humans in arbitrary poses and wearing any clothing, does not require the two people to be scanned from similar viewpoints, and runs in real time. We use a deep convolutional neural network to train a feature descriptor on depth map pixels, but crucially, rather than training the network to solve the shape correspondence problem directly, we train it to solve a body region classification problem, modified to increase the smoothness of the learned descriptors near region boundaries. This approach ensures that nearby points on the human body are nearby in feature space, and vice versa, rendering the feature descriptor suitable for computing dense correspondences between the scans. We validate our method on real and synthetic data for both clothed and unclothed humans, and show that our correspondences are more robust than is possible with state-of-the-art unsupervised methods, and more accurate than those found using methods that require full watertight 3D geometry. |
|
Reconciling Elastic and Equilibrium Methods for Static Analysis
Hijung V. Shin, Christopher F. Porst, Etienne Vouga, John Ochsendorf, and Frédo Durand ACM Transactions on Graphics, 2016 We examine two widely used classes of methods for static analysis of masonry buildings: linear elasticity analysis using finite elements and equilibrium methods. It is often claimed in the literature that finite element analysis is less accurate than equilibrium analysis when it comes to masonry analysis; we examine and qualify this claimed inaccuracy, provide a systematic explanation for the discrepancy observed between their results, and present a unified formulation of the two approaches to stability analysis. We prove that both approaches can be viewed as equivalent, dual methods for getting the same answer to the same problem. We validate our observations with simulations and physical tilt experiments of structures. |
|
Nested Cages
Leonardo Sacht, Etienne Vouga, and Alec Jacobson SIGGRAPH Asia ( ACM Transactions on Graphics ), 2015 Many tasks in geometry processing and physical simulation benefit from multiresolution hierarchies. One important characteristic across a variety of applications is that coarser layers strictly encage finer layers, nesting one another. Existing techniques such as surface mesh decimation, voxelization, or contouring distance level sets do not provide sufficient control over the quality of the output surfaces while maintaining strict nesting. We propose a solution that enables use of application-specific decimation and quality metrics. The method constructs each next-coarsest level of the hierarchy, using a sequence of decimation, flow, and contact-aware optimization steps. From coarse to fine, each layer then fully encages the next while retaining a snug fit. The method is applicable to a wide variety of shapes of complex geometry and topology. We demonstrate the effectiveness of our nested cages not only for multigrid solvers, but also for conservative collision detection, domain discretization for elastic simulation, and cage-based geometric modeling. |
|
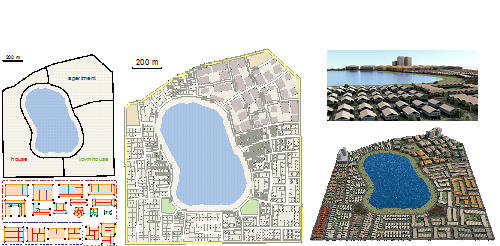
Urban Pattern: Layout Design by Hierarchical Domain Splitting
Y. L. Yang, J. Wang, Etienne Vouga, and Peter Wonka SIGGRAPH Asia ( ACM Transactions on Graphics ), 2013 We present a framework for generating street networks and parcel layouts. Our goal is the generation of high-quality layouts that can be used for urban planning and virtual environments. We propose a solution based on hierarchical domain splitting using two splitting types: streamline-based splitting, which splits a region along one or multiple streamlines of a cross field, and template-based splitting, which warps pre-designed templates to a region and uses the interior geometry of the template as the splitting lines. We combine these two splitting approaches into a hierarchical framework, providing automatic and interactive tools to explore the design space. |
|
3D Self-Portraits
Hao Li, Etienne Vouga, Anton Gudym, Jonathan T. Barron, Linjie Luo, Gleb Gusev SIGGRAPH Asia ( ACM Transactions on Graphics ), 2013 We develop an automatic pipeline that allows ordinary users to capture complete and fully textured 3D models of themselves in minutes, using only a single Kinect sensor, in the uncontrolled lighting environment of their own home. Our method requires neither a turntable nor a second operator, and is robust to the small deformations and changes of pose that inevitably arise during scanning. After the users rotate themselves with the same pose for a few scans from different views, our system stitches together the captured scans using multi-view non-rigid registration, and produces watertight final models. To ensure consistent texturing, we recover the underlying albedo from each scanned texture and generate seamless global textures using Poisson blending. Despite the minimal requirements we place on the hardware and users, our method is suitable for full body capture of challenging scenes that cannot be handled well using previous methods, such as those involving loose clothing, complex poses, and props. |
|
Diamonds from the Rough: Improving Drawing, Painting, and Singing via Crowdsourcing
Yotam Gingold, Etienne Vouga, Eitan Grinspun, and Haym Hirsh Proceedings of the AAAI Workshop on Human Computation (HCOMP), 2012 It is well established that in certain domains, noisy inputs can be reliably combined to obtain a better answer than any individual. It is now possible to consider the crowdsourcing of physical actions, commonly used for creative expressions such as drawing, shading, and singing. We provide algorithms for converting low-quality input obtained from the physical actions of a crowd into high-quality output. The inputs take the form of line drawings, shaded images, and songs. We investigate single-individual crowds (multiple inputs from a single human) and multiple-individual crowds. |
|
Speculative Parallel Asynchronous Contact Mechanics
Samantha Ainsley, Etienne Vouga, Eitan Grinspun, and Rasmus Tamstorf SIGGRAPH Asia ( ACM Transactions on Graphics ), 2012 We extend the Asynchronous Contact Mechanics algorithm and improve its performance by two orders of magnitude, using only optimizations that do not compromise ACM's three guarantees of safety, progress, and correctness. The key to this speedup is replacing ACM's timid, forward-looking mechanism for detecting collisions--locating and rescheduling separating plane kinetic data structures--with an optimistic speculative method inspired by Mirtich's rigid body Time Warp algorithm. Time warp allows us to perform collision detection over a window of time containing many of ACM's asynchronous trajectory changes; in this way we cull away large intervals as being collision free. Moreover, by replacing force processing intermingled with KDS rescheduling by windows of pure processing followed by collision detection, we transform an algorithm that is very difficult to parallelize into one that is embarrassingly parallel. |
|
Reflections on Simultaneous Impact
Breannan Smith, Danny Kaufman, Etienne Vouga, Rasmus Tamstorf, and Eitan Grinspun SIGGRAPH ( ACM Transactions on Graphics ), 2012 Resolving simultaneous impacts is an open and significant problem in collision response modeling. Existing algorithms in this domain fail to fulfill at least one of five physical desiderata. To address this we present a simple generalized impact model motivated by both the successes and pitfalls of two popular approaches: pair-wise propagation and linear complementarity models. Our algorithm is the first to satisfy all identified desiderata, including simultaneously guaranteeing symmetry preservation, kinetic energy conservation, and allowing break-away. Furthermore, we address the associated problem of inelastic collapse, proposing a complementary generalized restitution model that eliminates this source of nontermination. We then consider the application of our models to the synchronous time-integration of large-scale assemblies of impacting rigid bodies. To enable such simulations we formulate a consistent frictional impact model that continues to satisfy the desiderata. Finally, we validate our proposed algorithm by correctly capturing the observed characteristics of physical experiments including the phenomenon of extended patterns in vertically oscillated granular materials. |
|
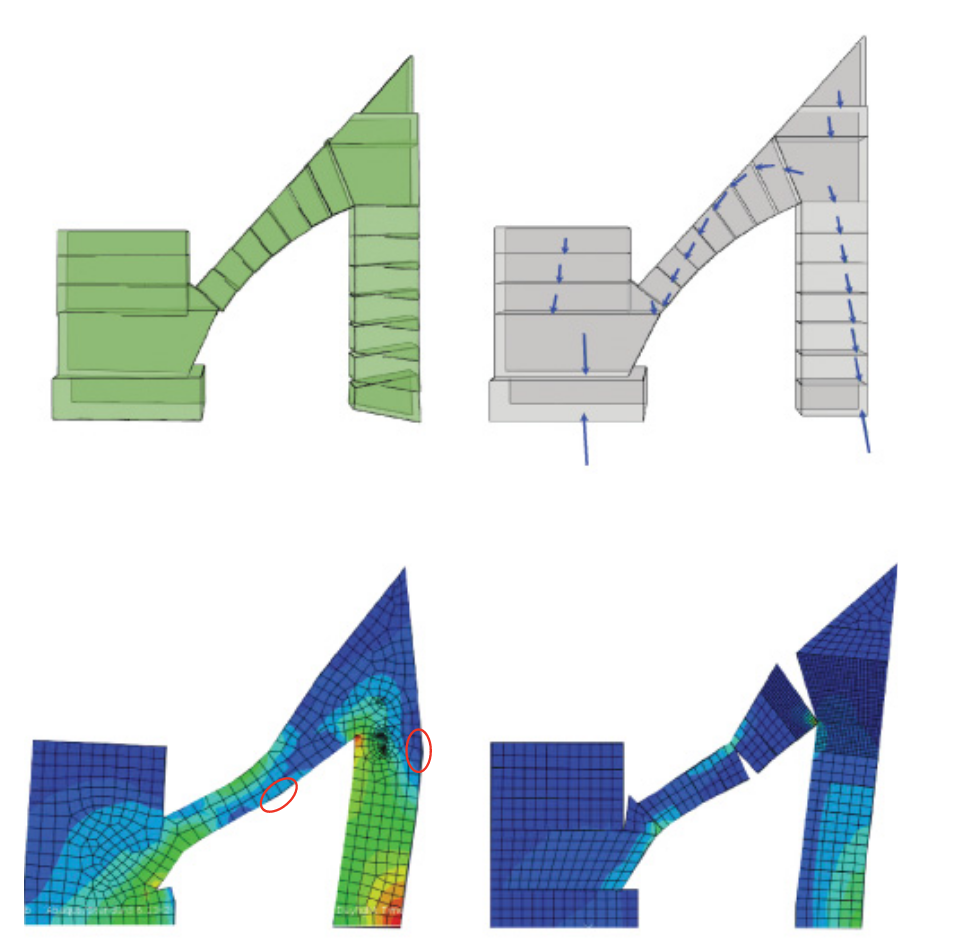
Design of Self-supporting Surfaces
Etienne Vouga, Mathias Höbinger, Johannes Wallner, and Helmut Pottmann SIGGRAPH ( ACM Transactions on Graphics ), 2012 Self-supporting masonry is one of the most ancient and elegant techniques for building curved shapes. Because of the very geometric nature of their failure, analyzing and modeling such strutures is more a geometry processing problem than one of classical continuum mechanics. This paper uses the thrust network method of analysis and presents an iterative nonlinear optimization algorithm for efficiently approximating freeform shapes by self-supporting ones. The rich geometry of thrust networks leads us to close connections between diverse topics in discrete differential geometry, such as a finite-element discretization of the Airy stress potential, perfect graph Laplacians, and computing admissible loads via curvatures of polyhedral surfaces. This geometric viewpoint allows us, in particular, to remesh self-supporting shapes by self-supporting quad meshes with planar faces, and leads to another application of the theory: steel/glass constructions with low moments in nodes. |
|
|
|
Flexible Developable Surfaces
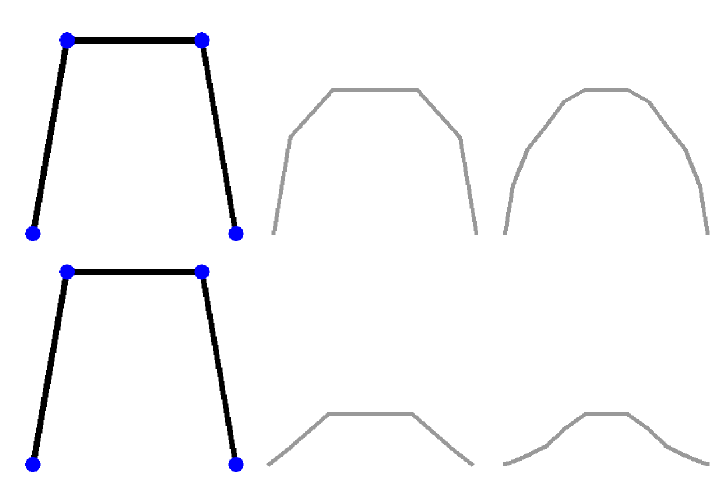
Justin Solomon, Etienne Vouga, Max Wardetzky, and Eitan Grinspun Eurographics Symposium on Geometry Processing, 2012 We introduce a discrete paradigm for developable surface modeling. Unlike previous attempts at interactive developable surface modeling, our system is able to enforce exact developability at every step, ensuring that users do not inadvertently suggest configurations that leave the manifold of admissible folds of a flat two-dimensional sheet. With methods for navigation of this highly nonlinear constraint space in place, we show how to formulate a discrete mean curvature bending energy measuring how far a given discrete developable surface is from being flat. This energy enables relaxation of user-generated configurations and suggests a straightforward subdivision scheme that produces admissible smoothed versions of bent regions of our discrete developable surfaces. |
|
Asynchronous Variational Contact Mechanics
Etienne Vouga, David Harmon, Rasmus Tamstorf, and Eitan Grinspun Computer Methods in Applied Mechanics and Engineering, 2011 An asynchronous, variational method for simulating elastica in complex contact and impact scenarios is developed. Asynchronous Variational Integrators (AVIs) are extended to handle contact forces by associating dierent time steps to forces instead of to spatial elements. By discretizing a barrier potential by an innite sum of nested quadratic potentials, these extended AVIs are used to resolve contact while obeying momentum- and energy-conservation laws. A series of two- and three-dimensional examples illustrate the robustness and good energy behavior of the method. |
|
Discrete Viscous Threads
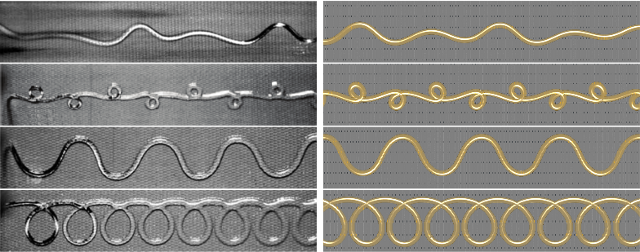
Miklos Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, and Eitan Grinspun SIGGRAPH ( ACM Transactions on Graphics ), 2010 We present a continuum-based discrete model for thin threads of viscous fluid by drawing upon the Rayleigh analogy to elastic rods, demonstrating canonical coiling, folding, and breakup in dynamic simulations. Our derivation emphasizes space-time symmetry, which sheds light on the role of time-parallel transport eliminating in approximation without all but an O(n) band of entries of the physical system's energy Hessian. The result is a fast, unified, implicit treatment of viscous threads and elastic rods that closely reproduces a variety of fascinating physical phenomena, including hysteretic transitions between coiling regimes, competition between surface tension and gravity, and the first numerical fluid-mechanical sewing machine. The novel implicit treatment also yields an order of magnitude speedup in our elastic rod dynamics. |
|
Asynchronous Contact Mechanics
David Harmon, Etienne Vouga, Breannan Smith, Rasmus Tamstorf, and Eitan Grinspun SIGGRAPH ( ACM Transactions on Graphics ), 2009 We develop a method for reliable simulation of elastica in complex contact scenarios. Our focus is on firmly establishing three parameter-independent guarantees: that simulations of well-posed problems (a) have no interpenetrations, (b) obey causality, momentum- and energy-conservation laws, and (c) complete in finite time. We achieve these guarantees through a novel synthesis of asynchronous variational integrators, kinetic data structures, and a discretization of the contact barrier potential by an infinite sum of nested quadratic potentials. In a series of two- and three-dimensional examples, we illustrate that this method more easily handles challenging problems involving complex contact geometries, sharp features, and sliding during extremely tight contact. |
|
On the Smoothness of Real-Valued Functions Generated by Subdivision Schemes Using Nonlinear Binary Averaging
Ron Goldman, Etienne Vouga, and Scott Schaefer Computer Aided Geometric Design, 2009 Our main result is that two point interpolatory subdivision schemes using C^k nonlinear averaging rules on pairs of real numbers generate real-valued functions that are also C^k. The significance of this result is the following consequence: Suppose that S is a subdivision algorithm operating on sequences of real numbers using linear binary averaging that generates C^m real-valued functions and S is the same subdivision procedure where linear binary averaging is replaced everywhere in the algorithm by a C^n nonlinear binary averaging rule on pairs of real numbers; then the functions generated by the nonlinear subdivision scheme S are C^k , where k = min(m, n). |
|
Robust Treatment of Simultaneous Collisions
David Harmon, Etienne Vouga, Rasmus Tamstorf, and Eitan Grinspun SIGGRAPH ( ACM Transactions on Graphics ), 2008 Robust treatment of complex collisions is a challenging problem in cloth simulation. Some state of the art methods resolve collisions iteratively, invoking a fail-safe when a bound on iteration count is exceeded. The best-known fail-safe rigidifies the contact region, causing simulation artifacts. We present a fail-safe that cancels impact but not sliding motion, considerably reducing artificial dissipation. We equip the proposed fail-safe with an approximation of Coulomb friction, allowing finer control of sliding dissipation. |
|
Nonlinear Subdivision Through Nonlinear Averaging
Scott Schaefer S, Etienne Vouga, and Ron Goldman Computer Aided Geometric Design, 2008 We investigate a general class of nonlinear subdivision algorithms for functions of a real or complex variable built from linear subdivision algorithms by replacing binary linear averages such as the arithmetic mean by binary nonlinear averages such as the geometric mean. Using our method, we can easily create stationary subdivision schemes for Gaussian functions, spiral curves, and circles with uniform parametrizations. More generally, we show that stationary subdivision schemes for e^p(x), cos(p(x)) and sin(p(x)) for any polynomial or piecewise polynomial p(x) can be generated using only addition, subtraction, multiplication, and square roots. The smoothness of our nonlinear subdivision schemes is inherited from the smoothness of the original linear subdivision schemes and the differentiability of the corresponding nonlinear averaging rules. While our results are quite general, our proofs are elementary, based mainly on the observation that generic nonlinear averaging rules on a pair of real or complex numbers can be constructed by conjugating linear averaging rules with locally invertible nonlinear maps. In a forthcoming paper we show that every continuous nonlinear averaging rule on a pair of real or complex numbers can be constructed by conjugating a linear averaging rule with an associated continuous locally invertible nonlinear map. Thus the averaging rules considered in this paper are actually the general case. As an application we show how to apply our nonlinear subdivision algorithms to intersect some common transcendental functions. |