Step 2: Determine the loop-invariant
(continued)
Now,
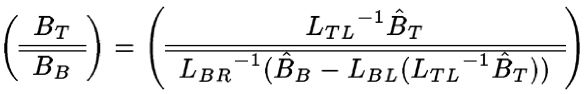 ,
,
represents all computation that must be performed to
update all of B with the final result, in terms
of the partitioned matrices.
The important observation is that at an intermediate step
only some of the operations have been performed towards
this final result.
Reasonable intermediate results would be
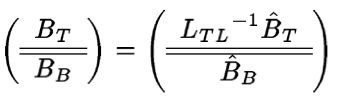 and
and
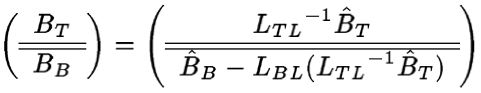 .
.
We will call the state on the left Loop-invariant 1
and the one on the right Loop-invariant 2,
or Invariant 1 and 2, for short.
We will continue our discussion by considering Invariant 2
We will prescribe that this state be maintained at the following
four points in the algorithm (as indicated by Step 4 in the worksheet):
-
Before the loop commences;
-
At the top of the loop;
-
At the bottom of the loop; and
-
Immediately after exiting the loop.
[
UPDATE SOURCE
]
[
VIEW
PDF
PS
]
[
BACK
]
[
NEXT
]
![]() ,
,
![]() and
and
![]() .
.