Skip to main content

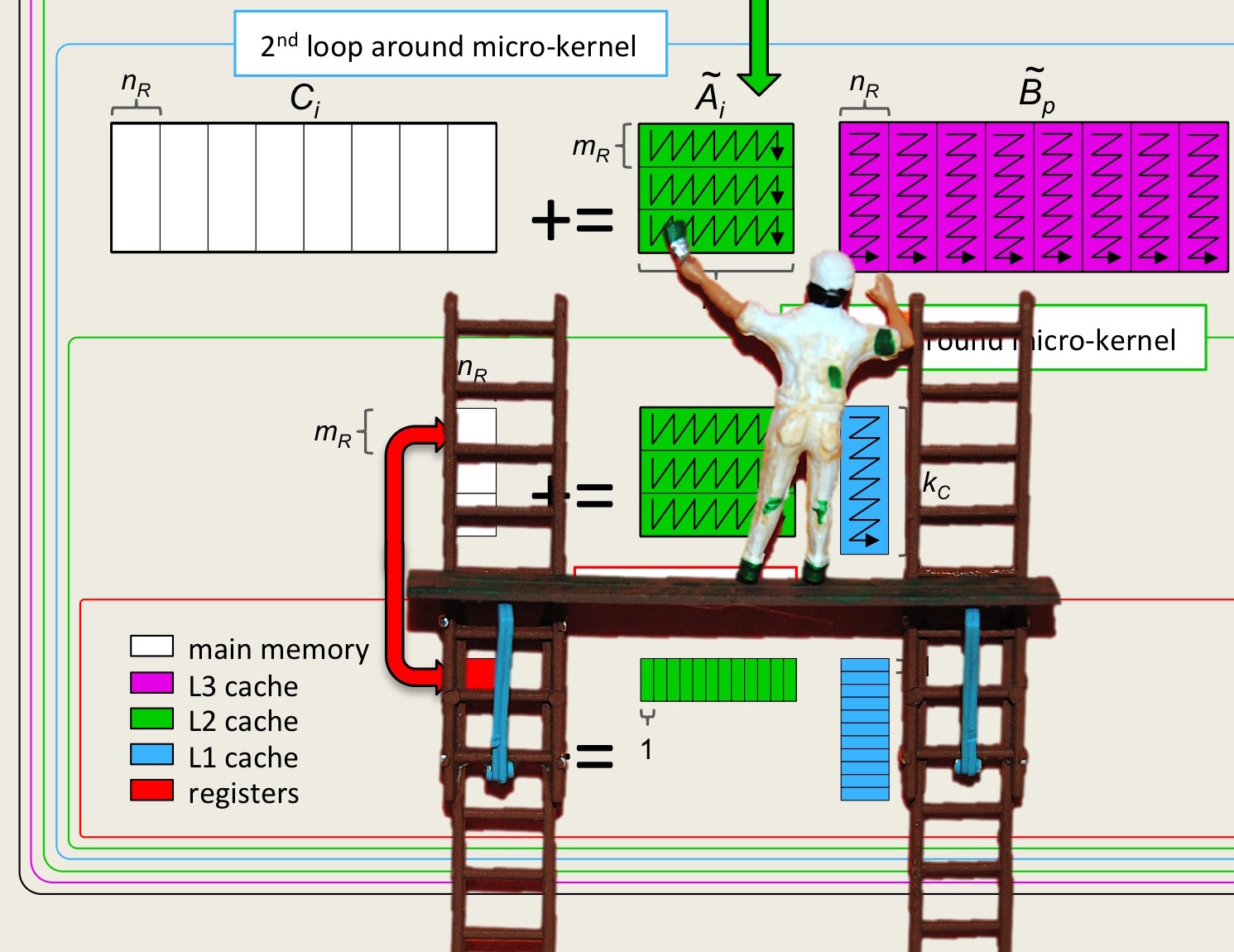
Unit 2.3.3 Streaming \(A_{i,p} \) and \(B_{p,j} \)

Now, if the submatrix \(C_{i,j} \) were larger (i.e., \(m_R \) and \(n_R \) were larger), then the time spent moving data around (overhead),

\begin{equation*} \left[ 2 m n + m n k ( \frac{1}{n_R} + \frac{1}{m_R} ) \right] \beta_{R \leftrightarrow M}, \end{equation*}

is reduced:

\begin{equation*} \frac{1}{n_R} + \frac{1}{m_R} \end{equation*}

decreases as \(m_R \) and \(n_R \) increase. In other words, the larger the submatrix of \(C \) that is kept in registers, the lower the overhead (under our model). Before we increase \(m_R \) and \(n_R \text{,}\) we first show how for fixed \(m_R \) and \(n_R \) the number of registers that are needed for storing elements of \(A \) and \(B \) can be reduced, which then allows \(m_R \) and \(n_R \) to (later this week) be increased in size.

Recall from Week 1 that if the \(p \) loop of matrix-matrix multiplication is the outer-most loop, then the inner two loops implement a rank-1 update. If we do this for the kernel, then the result is illustrated by

If we now consider the computation

we recognize that after each rank-1 update, the column of \(A_{i,p} \) and row of \(B_{p,j} \) that participate in that rank-1 update are not needed again in the computation of \(C_{i,j} := A_{i,p} B_{p,j} + C_{i,j} \text{.}\) Thus, only room for one such column of \(A_{i,p}\) and one such row of \(B_{p,j} \) needs to be reserved in the registers, reducing the total number of doubles that need to be stored in registers to

\begin{equation*} m_R \times n_R + m_R + n_R. \end{equation*}

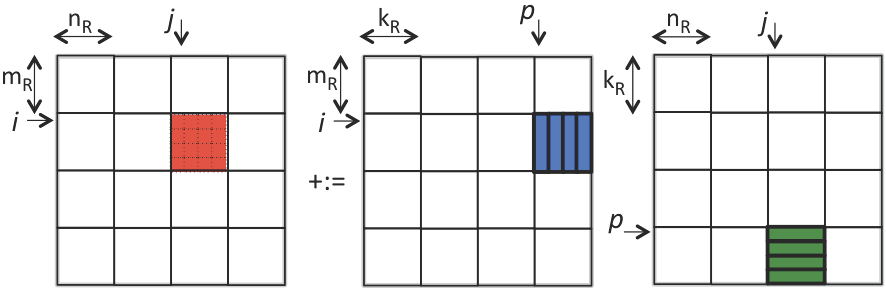
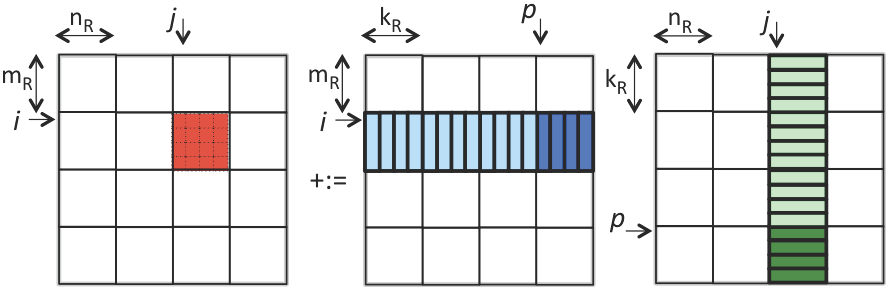
If \(m_R = n_R = 4 \) this means that \(16 + 4 + 4 = 24 \) doubles in registers. If we now view the entire computation performed by the loop indexed with \(p \text{,}\) this can be illustrated by

and implemented as

void MyGemm( int m, int n, int k, double *A, int ldA,
			  double *B, int ldB, double *C, int ldC )
{
  for ( int i=0; i<m; i+=MR ) /* m assumed to be multiple of MR */
    for ( int j=0; j<n; j+=NR ) /* n assumed to be multiple of NR */
      for ( int p=0; p<k; p+=KR ) /* k assumed to be multiple of KR */
	Gemm_P_Ger( MR, NR, KR, &alpha( i,p ), ldA,
			        &beta( p,j ), ldB, &gamma( i,j ), ldC );
}

void Gemm_P_Ger( int m, int n, int k, double *A, int ldA,
		      double *B, int ldB, double *C, int ldC )
{
  for ( int p=0; p<k; p++ )
    MyGer( m, n, &alpha( 0,p ), 1, &beta( p,0 ), ldB, C, ldC );
}
Figure 2.3.5. Blocked matrix-matrix multiplication with kernel that casts \(C_{i,j} = A_{i,p} B_{p,j} + C_{i,j} \) in terms of rank-1 updates.
Homework 2.3.3.1.

In directory Assignments/Week2/C examine the file Assignments/Week2/C/Gemm_JIP_P_Ger.c Execute it with 

make JIP_P_Ger

and view its performance with Assignments/Week2/C/data/Plot_register_blocking.mlx.

Solution

This is the performance on Robert's laptop, with MB=NB=KB=4:

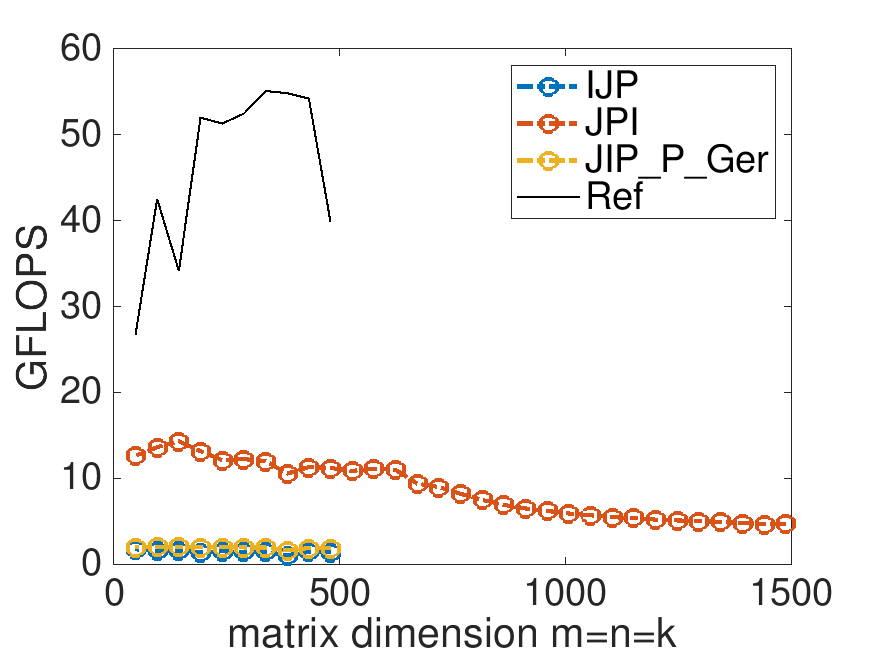
The performance is pathetic. It will improve!

It is tempting to start playing with the parameters MB, NB, and KB. However, the point of this exercise is to illustrate the discussion about casting the multiplication with the blocks in terms of a loop around rank-1 updates.

Remark 2.3.6.

The purpose of this implementation is to emphasize, again, that the matrix-matrix multiplication with blocks can be orchestratred as a loop around rank-1 updates, as you already learned in Unit 1.4.2.

login