|
Hyung Joon Kook Department of Computer Science King Sejong University Seoul, Korea 133-747 |
Gordon S. Novak Jr.
Department of Computer Sciences University of Texas at Austin Austin, TX 78712 |
Copyright © 1991 by IEEE.
Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from the IEEE.
This article appears in IEEE Transactions on Knowledge and Data Engineering, vol. 3, no. 1, March 1991, pp. 48-54.
This research was supported by the U.S. Army Research Office under contract DAAG29-84-K-0060. Computer equipment used in this research was donated by Xerox Corporation and Hewlett Packard.
Expertise in solving physics problems is characterized by the ability to set up or represent a problem. An expert's representation employs idealized formal models, such as a point mass or the principle of uniform circular motion, for modeling objects and relationships in the problem. A computer program, APEX, has been developed to investigate such models. Two types of models are defined: canonical physical objects and physical models. During problem solving, the problem is represented as a data connection network, which is progressively augmented by these models in the form of additional network elements. APEX employs views as a representational framework for connecting the initially informal objects to the formal models of the domain. The view framework supports multiple representations (e.g., viewing many objects as a single canonical physical object), handling of incompletely specified problems, and invertability of the views. This computational framework provides a powerful representational mechanism that allows a finite set of physical principles to be applied to a potentially infinite variety of problems. As a knowledge engineering technique, views allow general principles to be applied to a variety of objects whose representations differ.
Physics problems are often presented in terms of informal, real-world objects and relationships among them. An important task of a problem solver is to obtain a formal representation of the problem by interpreting these objects and relationships into formal, abstract models of physics. Competence in solving a physics problem derives mainly from the skill of setting up the problem in terms of these models, rather than from mere mathematical skill [larkin:lmss]. An expert in physics is believed to possess a finite set of such models that may be applied to solve a large number of complex problems.
We have been investigating a machine problem solver in physics with representation and model-building as the primary research issues [kook:diss]. APEX (A Physics Expert) is a computer program built in an object-oriented programming environment [novak:glisp] for solving physics problems in a model-based representational framework. Two types of models are employed in APEX: canonical physical objects and physical models. Canonical physical objects are idealized objects that are meaningful in physics or mathematics, such as a point mass, a circle or an ideal rope. Physical models are data structures for representing the laws and principles of physics.
APEX extends the work in ISAAC [novak:isaac,novak:ijcai], a program that solves physics problems stated in English, with the main research issue shifted from natural language understanding to representational aspects of physics problem solving. Many underlying ideas in APEX are supported by psychological research [chi], in which experts and novices were compared in categorizing a given set of problems. Other studies of performance differences between experts and novices [larkin:etal,larkin] suggest the importance of model-building behavior of experts. [addanki] and [murthy] describe the use of graphs that relate physical models, with edges of a graph representing differences in the assumptions of the models. [lowry] describes abstraction models in the domain of programming. [bobrow] includes descriptions of several approaches to qualitative reasoning about physical systems, including qualitative process theory [forbus], confluences [dekleer-brown], and qualitative simulation [kuipers]. Whether the models used are purely quantitative or are qualitative, a central issue is the model formulation process that we address; it is crucial when dealing with problems that are presented in the informal terms of the real world, often incompletely specified.
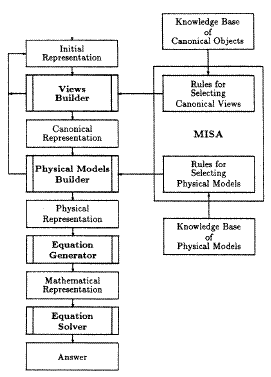
The organization of the program and its data is shown in Figure 1. In the diagram, programs are represented by boxes with double lines, and data structures and rules by plain boxes; links between boxes represent data flow.

Fig. 1: Overall Program Organization.
A physics problem is input as a semantic network describing features of objects and their relationships. The inputs used in testing APEX were hand-simulations of the output of a hypothetical English parser similar to those of ISAAC [novak:isaac] and BEATRIX [novak-bulko,bulko,bulko:diss]. In one case, the output of BEATRIX was mechanically reformatted to serve as input to APEX.
Given an initial representation of a problem, the process of solving it occurs in several steps. First, guided by an inference system that reasons about the objects and their interactions, APEX transforms the initial problem into a representation in terms of canonical physical objects, such as a point mass, selected from a library. This transformation is performed by constructing a data connection network between the two objects that provides a computational facility for viewing an object as another (canonical physical) object. Therefore, the problem representation resulting from this stage (labeled canonical representation in the diagram) actually consists of a group of views that inherit all the properties of corresponding canonical physical objects.
Then, the canonical representation is again used as input for reasoning by the inference system, which guides APEX in building a physical representation of the problem in which the underlying physical principles and laws involved in the problem are explicitly represented. APEX's physical models can be divided into two subgroups based on their operational goals: those specialized for making inferences about implicit forces, and those specialized for writing equations. Accordingly, this stage of problem solving is performed in two distinct steps; the first step is to select and instantiate physical models involving forces, and the second step is to select and instantiate physical models involving equations.
Next, a mathematical representation of the problem is formulated by collecting equations from the physical model instances in the physical representation. Finally, the equations, which may contain symbolic constants as well as numbers (with units) and variables, are sent to a symbolic manipulation package designed to solve simultaneous equations.
As outlined above, APEX solves a physics problem by a series of stepwise re-representation processes involving invocations of models to the initial problem representation. This process augments the previous problem representation rather than replacing it. Therefore, the final problem representation may be considered a representation of the problem with full specification of its underlying structures that were initially implicit. At each stage, APEX must be guided to select proper canonical objects or physical models. This guidance may be provided by a human, through a user-friendly interface, or by an expert system. MISA (Mini Inference System for APEX) is a small expert system that has been developed to demonstrate APEX in a limited number of problem-solving sessions without human intervention. MISA comprises of a set of inference rules that a human physics expert might consider when selecting proper models.
Canonical objects such as a point mass, a lever, or an ideal rope serve as the vocabulary for physics; problem solving requires interpreting the objects in the initial problem into these canonical objects. A group of canonical objects has been predefined in APEX's permanent knowledge base; each is an object class in an object-oriented programming environment. A canonical object class is defined with intrinsic attributes and methods for computing properties from the attributes. Figure 2 shows the definitions for some canonical object classes.
| class: | PtMass |
| attributes: | mass |
| superclass: | CanonicalObj |
| class: | Rope |
| attributes: | rotation |
| tension | |
| superclass: | CanonicalObj |
| class: | Circle |
| attributes: | radius |
| properties: | diameter <- 2 * radius |
| area <- pi * radius2 | |
| perimeter <- pi * diameter | |
| superclass: | CanonicalObj |
Fig. 2: Example Canonical Object Classes.
We regard the process of abstracting an initial object as a canonical physical object as a data conversion process, accomplished by views. A view serves as a hybrid data structure facilitating bidirectional mapping of the features of the objects in the two representations. Viewing an input object as a canonical object is achieved by constructing a collection of network elements within the object-oriented programming environment of APEX. The network consists of five kinds of data elements:
A car is moving on a circular racetrack with a curvature-radius of 60m. If the banking of the racetrack is 30 degrees from the horizontal, what is the uniform speed of the car to keep it moving in the circle without friction?In solving the problem, MISA (Mini Inference System for APEX) suggests a circle view of the track, among other views. Figure 3 shows the view network constructed by APEX for that effect. In the diagram, a real-world object instance, Racetrack1, is abstracted as a canonical object class, Circle. A new view class, CircleView1, is constructed with an originalobj attribute and a radius property. The mapping instruction for deriving the feature of the target canonical object, i.e., radius, is given by MISA as (GETV Racetrack1 curvature-radius). [ (GETV < obj> < slot> ) retrieves the value of < slot> from < obj> .] This mapping instruction is then stored, in a more general form, (GETV originalobj curvature-radius), in the CircleView1 class as the method for computing its radius property. The internal data structure for the CircleView1 class is shown in Figure 4. Finally, an instance of the view class, CircleView1.1, is created with its originalobj attribute defined as Racetrack1.
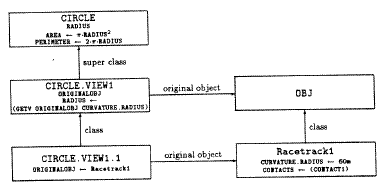
Fig. 3: An Example View Network Structure.
| class: | CircleView1 |
| attributes: | originalobj |
| viewdescription | |
| properties: | radius <- (GETV originalobj curvature-radius) |
| superclass: | Circle |
| View | |
Fig. 4: Data Structure for CircleView1.
The resulting view instance, once constructed, enables APEX to treat it as if it were a `real' Circle, i.e., properties of a Circle (e.g., area, perimeter) are directly accessible to the view instance thanks to the property inheritance mechanism of the object-oriented programming environment. In APEX, the final physical representation of a problem is obtained in terms of a collection of such view instances.
Physics problems are often incompletely specified. Such under-specification is effectively dealt with by the proposed representational framework. APEX's canonical representations provide bidirectional data conversion between the initial and canonical representations of a problem. In the forward direction (from initial to canonical, and to physical representation), the derivation methods are stored only in symbolic forms specifying where and how to derive data. Actual values are not retrieved until after building the final physical representation of the problem, at which point values are retrieved by evaluating these forms in order to write equations involving only constants and variables. In the backward direction, intermediate results obtained from the canonical (or physical) representation are transmitted into the missing slots of the original representation, eventually resulting in full specification of the problem. An example of backward data propagation would be when external forces acting on the car (viewed as a point mass) in the previous example are considered. In order to derive the gravitational force exerted on the car, it is necessary to consider the gravitational field in which the car resides. For this, APEX decides to create a field instance with default gravitational constant; the newly created instance is attached to the car in the initial representation. [A field is an environment of an object. In APEX, there are four kinds of environments: field, contact, motion and external force.] In an analogous way, backward data propagations are also effectively used for specifying an object's structural attributes (e.g., the tension of a rope), or even attributes of an environment (e.g., the acceleration of a motion).
[novak:mult] suggested the importance of multiple representations in solving physics problems. In the previous section, we discussed viewing a single object as a single canonical object. As problem complexity increases, however, there are cases in which a one-to-one view strategy alone is not adequate. This occurs when an object plays multiple roles in the problem; for example, in the racetrack problem, the track's geometry must be abstracted as a canonical circle and viewed as a canonical incline as well. This type of multiple view (one-to-many view) is handled in APEX without any difficulty, since once a canonical views representation is constructed, its internal data connections to initial objects are transparent to the problem solver.
Another type of multiple view is viewing many objects as a single canonical object. Representation of many-to-one views requires additions to the view framework we have presented. We will describe the extensions to the proposed view framework by considering the following problem [larkin].
What constant horizontal force F must be applied to the large cart in Figure 5 (of mass M) so that the smaller carts (masses m1 and m2) do not move relative to the large cart? Neglect friction.
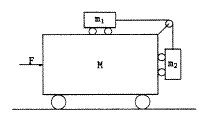
Fig. 5: Sample Problem.
In solving this problem, the problem solver must take a single point mass view of all objects in motion (three carts, pulley and string) as a preliminary step to writing a force equation about the total mass with respect to the external force (F). When advised by the inference system to view these objects as a point mass, APEX's canonical representation builder first recognizes this as advice to build a many-to-one view network and makes an instance of CompositeObj class in the current context. CompositeObj is a special object class that is designed to bridge between a target canonical view and multiple objects in the initial representation. An instance of the CompositeObj class is essentially an encapsulation of multiple objects, with pointers to those objects involved in the view. Once such an instance is set up, it is treated by APEX as a single object instance for the later stages of problem solving. Figure 6 shows the problem representation after a multiple view is taken (the initial problem representation is shown in the dashed box). Figure 7 shows the data structures for the added nodes.
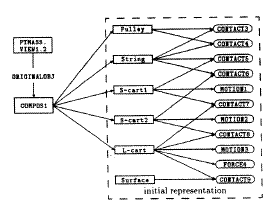
Fig. 6: Multiple View.
| instance: | PtMassView1.2 |
| attributes: | originalobj <- CompositeObj1 |
| viewdescription <- ViewDesc1 | |
| properties: | mass <- (GETV originalobj mass) |
| superclass: | PtMass |
| View |
| instance: | CompositeObj1 |
| attributes: | fromobjs <- (S-cart1 S-cart2 L-cart Pulley String) |
| properties: | mass <- M + m1 + m2 |
Fig. 7: Data Structures for the Elements of Multiple View.
A physics textbook presents a set of physical principles. Expertise in problem solving requires the ability to apply a proper set of physical principles, in order to obtain a set of equations relevant to the problem. APEX employs physical models as the data structures for modeling principles of physics. A physical model is an encapsulation of a single principle or law of physics, stored in a permanent knowledge base of APEX. Whereas a canonical physical object is an abstraction of one or more objects, a physical model is a physical interpretation of a situation involving objects and their relationships. Each physical model contains a chunk of physical principle such as:
Physical models are implemented as a set of object classes in an object-oriented programming environment. The following is the description of the contents of a physical model.
When the inference system (e.g., MISA) examines the canonical representation of a problem for selecting physical models, the components of physical models are tested for match with a certain group of views and their environments. If a physical model involving a sysvar (e.g., a coordinate system) is selected, the inference system first computes it by invoking a library procedure specialized for this task.
After matching contexts (and sysvar, if any) are passed to programs for instantiating the selected physical models, these programs first construct an object class called a model class by copying from the attributes of the selected physical model with an additional attribute for model description. After making the new model class a subclass of the selected physical model, the model-building programs instantiate it in the given context. The locals of the physical model (which is now a super class of the model class) are computed in a predefined order using the methods given in the locals property definitions; this may involve inference of unspecified data. Suppose, for instance, that the physical model in Figure pmex1 has been selected for instantiation, and that the obj in question is in contact (Contact1) with the incline in question. If the normal force acting at Contact1 is initially unknown, the effect of computing
(GETV contact normalforce
(CREATE Vector WITH dir = (normalto incline)))
is to create a vector as prescribed by the (CREATE ...)
procedure (i.e., with direction = (normalto incline) and
magnitude = a symbolic constant), and to store it as
the value of the normalforce property of Contact1.
| class: | NormalforceModel |
| components: | obj |
| incline | |
| property: | contact <- (CONTACTBETWEEN obj incline) |
| loc <- (LOCATIONOF obj contact) | |
| force.vect <- (GETV contact normalforce (CREATE Vector WITH dir = (normalto incline))) | |
| force.env <-
(CREATE ExtForce WITH force = force.vect obj = obj loc = loc agent = incline) | |
| OUT <- (ENVADD obj force.env) | |
| superclass: | PhysicalModel |
Fig. 8: Physical Model Class NormalforceModel.
The last property of a physical model is always an OUT property. Computation of an OUT property results in generating either a set of equations (through an EQNADD operation) or a new environment for an object (through an ENVADD operation). When the OUT property is an EQNADD operation, the equations are stored in a global equation set. An example use of an ENVADD operation is given in Figure 8; instantiation of this model will result in attaching the force (an environment) to the obj. Hence, the net effect of selecting and instantiating a physical model is the formulation of a solution model which either explicates an implicit environment of an object or writes one or more constraint equations about an underlying structure of the problem. In APEX, a problem is finally solved by manipulating a set of constraint equations obtained from a selected set of physical model instances.
Selecting proper physical models requires what is sometimes called physical intuition [simon]; the problem solver, human or machine, may not rely merely on the surface features of the problem statement but often is required to reason about the underlying structures and principles of the given system [chi]. In APEX, such expertise is captured in a collection of inference rules, MISA (Mini Inference System for APEX), that reasons about the features and the contexts (e.g., environments) of objects in order to guide APEX in selecting views and physical models. MISA is a relatively small-scale rule base designed to work on a small number of selected physics problems for the purpose of demonstrating the ideas of APEX's representation [kook:diss].
In addition to automatic selection of models, a user-friendly interface to APEX has been developed to allow manual selection. When APEX is running in human-guided inference mode, MISA is turned off, and the representation choices for a problem are made according to instructions from the human user. The interface package also provides graphical presentations of the current state of APEX's internal representation of the problem, in which a graph node (e.g., a view or a physical model instance) may be further inspected in a menu-driven way. Figure 9 shows the screen image while solving the racetrack problem.
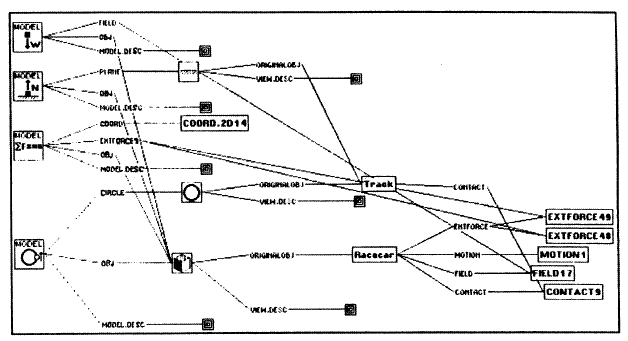
Fig. 9: Screen Image while Solving the Racetrack Problem.
As APEX solves a problem, the representation does not explicitly reflect the system's inference history that brought about the present state of problem representation. APEX employs view descriptions and model descriptions as data structures for keeping track of the system's inference history. View and model descriptions are defined as object classes, which are instantiated for specific viewing or modeling operations and attached to the resulting view or physical model. They record what rule has been applied to what kind of situations, and what initially-unspecified quantities have been derived and how. During or after solving a problem, they allow APEX to answer questions about the system's reasoning behavior. For instance, a user might want to ask the system why a specific view has been taken; through the menu-driven graphic interface, the user can obtain the answer in the form of a rule, instantiated in its matching context and translated into English.
This paper presents an advanced representation mechanism for physics problems. By isolating representation from inference, it allows the problem solver to choose which representations to use: those made by human user or those made by an expert system. Accomplishments of this research include development of formal representations for the conceptual entities [greeno] and relations of physics. The proposed representation separates views from actual objects in a way that facilitates invertibility of the view and multiple representations.
In this scheme, the internal representations of a problem is obtained as a collection of physical models which are constructed from the views and which are, in turn, connected to the informal representations of the original objects. Due to the transparency of the linkage between the physical models and the original objects, the physical models are made independent of the representations of the actual objects, which might contain a variety of informal features and relations of the real world. This scheme achieves an important goal of a computational model for solving physics problems: how can a finite set of physical principles suffice to solve an infinite set of problems?
The APEX system has been tested on five physics problems; details are given in [kook:diss]. We believe that the representational framework of APEX would be sufficient for a veriety of physics problems and for engineering domains in which problem solving is based on interaction of discrete canonical models of real-world objects; it would not be suitable for problems involving, e.g., fields that vary over space or time and that could not be modeled as discrete interactions among objects. The MISA expert system used to choose the models to be used for a given problem is a small one, and it would need considerable expansion to handle a wide variety of problems; this is an area of current research.
The representational methodologies and system design principles of this research may be useful for knowledge engineering in many application areas. As knowledge-based systems become larger and more widespread, the problem of reuse of knowledge becomes critical: How can general knowledge developed for one application be used in a different application, which may involve different representations for the objects? The view mechanism we describe allows the separation of the canonical view taken in coding the general principles from the representations of the objects to which these principles are applied. Because the views are bidirectional, it is possible not only to derive properties of objects as needed for reasoning, but to return the results of the reasoning to the original objects in the appropriate form. Views can therefore allow the development of expert knowedge to be decoupled from the applications to which it is applied.
[addanki] S. Addanki, R. Cremoni, and J. S. Penberthy, ``Reasoning About Assumptions in Graphs of Models,'' Proc. IJCAI-89, pp. 1432-1438.
[bobrow] Bobrow, D., ed., Qualitative Reasoning about Physical Systems, M.I.T. Press, 1985.
[bulko] W. Bulko. ``Understanding Text With an Accompanying Diagram'', Proc. First International Conference on Industrial and Engineering Applications of AI and Expert Systems, Tullahoma, TN, 1988, pp. 894-898.
[bulko:diss] William Bulko. Understanding Coreference in a System for Solving Physics Word Problems, Ph.D. dissertation, available as AI-89-102, CS Dept., Univ. of Texas at Austin, 1989.
[bundy:ai] A. Bundy. ``Will It Reach the Top? Prediction in the Mechanics World'', Artificial Intelligence, 10, 1978, pp. 129-146.
[chi] M. Chi, P. Feltovich and R. Glaser. ``Categorization and Representation of Physics Problems by Expert and Novices'', Cognitive Science, 5, 1981, pp. 121-152.
[dekleer-brown] J. de Kleer and J. S. Brown, ``A Qualitative Physics Based on Confluences'', in [bobrow], pp. 7-84.
[forbus] K. Forbus, ``Qualitative Process Theory'', in [bobrow], pp. 85-168.
[gentner] D. Gentner. and A. Stevens. (eds.) Mental Models. Hillsdale, NJ: Lawrence Erlbaum Associates, 1983.
[greeno] J. Greeno. ``Conceptual Entities'', in [Gentner and Stevens 83].
[halliday] D. Halliday and R. Resnick. Physics. New York, NY: John Wiley and Sons, 1978.
[kook:diss] H. J. Kook. A Model-Based Representational Framework for Expert Physics Problem Solving. Ph. D. dissertation. Available as AI-89-103, CS Dept., Univ. of Texas at Austin, 1989.
[kuipers] B. Kuipers, ``Commonsense Reasoning about Causality: Deriving Behavior from Structure'', in [bobrow], pp. 169-204.
[larkin:lmss] J. Larkin, J. McDermott, D. Simon and H. Simon. ``Expert and Novice Performance in Solving Physics Problems'', Science, 208, 20 June 1980, pp. 1335-1342.
[larkin:etal] J. Larkin, J. McDermott, D. Simon and H. Simon. ``Models of Competence in Solving Physics Problems'', Cognitive Science, 4, 1980, pp. 317-345.
[larkin] J. Larkin. ``The Role of Problem Representation in Physics'', In [Gentner and Stevens 83].
[lowry] M. Lowry, ``The Abstraction/Implementation Model of Problem Reformulation'', Proc. IJCAI-87, pp. 1004-1010.
[murthy] S. Murthy and S. Addanki, ``PROMPT: An Innovative Design Tool'', Proc. AAAI-87, pp. 637-642.
[novak:isaac] G. Novak. ``Computer Understanding of Physics Problems Stated in Natural Language'', American Journal of Computational Linguistics, Microfiche 53, 1976. Also available as TR-NL-30, CS Dept., Univ. of Texas at Austin, 1976.
[novak:ijcai] G. Novak. ``Representations of Knowledge in a Program for Solving Physics Problems'', Proc. IJCAI-77, 1977, pp. 286-291.
[novak:mult] G. Novak and A. Araya. ``Physics Problem Solving Using Multiple Views'', TR-173, CS Dept., Univ. of Texas at Austin, 1981.
[novak:glisp] G. Novak. ``GLISP: A LISP-Based Programming System With Data Abstraction'', AI Magazine, Fall, 1983, pp. 37-47.
[siegler] R. Siegler. (ed.) Children's Thinking: What Develops? Hillsdale, NJ: Lawrence Erlbaum Associates, 1978.
[simon] D. Simon and H. Simon. ``Individual Differences in Solving Physics Problems," in [siegler].