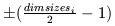Conversion of Units of Measurement
Gordon S. Novak Jr.
Department of Computer Sciences
University of Texas, Austin, TX 78712
Copyright © 1995 by IEEE.
Personal use of this material is permitted. However, permission to
reprint/republish this material for advertising or promotional purposes
or for creating new collective works for resale or redistribution to
servers or lists, or to reuse any copyrighted component of this work
in other works must be obtained from the IEEE.
This article appears in
IEEE Transactions on Software
Engineering, vol. 21, no. 8 (August 1995), pp. 651-661.
Abstract
Algorithms are presented for converting units of measurement from a
given form to a desired form. The algorithms are fast, are able
to convert any combination of units to any equivalent combination,
and perform dimensional analysis to ensure that the conversion is
legitimate. Algorithms are also presented for simplification of
symbolic combinations of units. Application of these techniques to
perform automatic unit conversion and unit checking in a programming
language is described.
Index Terms -- unit conversion, unit of measurement,
dimensional analysis, data type.
Introduction
Although many programming languages are described as ``strongly
typed'', in most languages the types of numeric quantities are
described only in terms of the numeric representation (real,
integer, etc.) but not in terms of the units of measurement
(meters, feet, etc.) of the quantity represented by a
variable. The assignment of a value represented in one unit to a
variable that is assumed to be in a different unit is clearly an
error, but such errors cannot be detected if the type system does not
include units of measurement. Conversion of units must be done
explicitly by the programmer; this can be both burdensome and
error-prone, since the conversion factors used by the programmer might
be entered incorrectly or might have limited accuracy. Failure to
represent units explicitly within program code is a serious
shortcoming in specification of the program, since later modification
of the program might be performed under the assumption of the wrong
units. Hundreds of units of measurement are in general use; entire
books [ackley] [horvath] [rossini] [semioli]
[wildi] are devoted to tables of unit conversions.
This paper presents methods for symbolic representation of units of
measurement.
Efficient algorithms are presented that can convert any
combination of units to any equivalent combination, while verifying
the legitimacy of the conversion by dimensional analysis.
Algorithms are also presented for simplification of combinations of
symbolic units. Applications of these techniques in programming
languages and in data conversion are discussed.
Related Work
Units and Unit Conversion
[nist330] and [iso-standard] describe the Syst`eme
International or International System of Units, abbreviated SI;
these are the definitive references on SI. [ansi-ieee-268]
provides style guidelines for use of SI units and tables of
conversion factors.
Several books provide conversion factors and algorithms for use in
unit conversion. The available books differ widely in the number of
units covered, the accuracy of the conversion factors, and the
algorithms that some books present for unit conversion. Although one
might think that unit conversion is easy and ``everyone knows how to
do it'', the number of books and the variety of methodologies and
algorithms they present suggest otherwise.
Horvath [horvath] has an especially complete coverage of
different units, as well as an extensive bibliography. The tables in
this book give conversion factors from a given unit to a single SI
unit; this is similar to the approach taken in the present paper,
although Horvath does not present conversion algorithms per se.
Semioli and Schubert [semioli] present voluminous tables that
combine multiplication of the conversion factor by the quantity of the
source unit to be converted. They also present somewhat complex
methods for obtaining additional accuracy and shifting the decimal
place of the result. This book has the flavor of a book of logarithm
tables, although it was published in 1974, when pocket calculators
were available.
Wildi [wildi] presents a series of directed acyclic graphs; each
node of a graph is a unit, and arcs between nodes are labeled with
conversion factors. The nodes are ordered by size of the unit. In
order to convert from one unit to another, the user traverses the
graph from the source unit to the goal unit, multiplying together all
the conversion factors encountered along the way (or dividing if
moving against the directed graph arrows). Although this technique
presents many conversions together in a compact structure, its use
involves many steps and thus many opportunities for error and loss of
accuracy.
Karr and Loveman [karr] outline a computational method for
finding conversion factors. Their method involves writing dimensional
quantities and conversion factors in terms of logarithms, making a
matrix of the equations in logarithmic form, and solving the matrix by
linear algebra. Since the size of the matrix is the number of units
involved in the conversion multiplied by the number of units the
system knows about, both the matrix and the time required to solve it
could quickly become large.
Schulz [schulz] describes COMET, an APL program for converting
measurements from the English system used in the U.S. to the metric
system. COMET focuses on conversion of machine part specifications
that include allowable tolerances.
Gruber and Olsen [gruber-olsen94] describe an ontology for
engineering mathematics, including representation of units of
measurement as an Abelian group. Their system can convert units,
presumably by a process of logical deduction that would be
significantly slower than the methods we describe.
Units in Programming Languages
Units of measurement are allowed in the ATLAS language [atlas],
although ATLAS allows only a limited set of units and a limited
language for constructing combinations of units.
Cunis [cunis92] describes Lisp programs for converting units.
These programs combine units with numeric measurements at runtime
and perform runtime conversion. While this is consistent with the
Lisp tradition of runtime type checking, it does not allow detection
of conversion errors at compile time. Gehani [gehani77] argues
in favor of compile-time checking.
Hilfinger [hilfinger88] describes methods for including units
with numeric data using Ada packages and discusses modifications of
Ada compilers that would be required to make use of these packages
efficient and allow compile-time checking of correctness of
conversions.
Karr and Loveman [karr] propose incorporation of units into
programming languages; they discuss methods of unit conversion,
dimensional analysis, and language syntax issues. We believe that
the unit conversion algorithms described in the present paper are
simpler: our methods require only one scalar operation per unit for
conversion and one scalar operation per unit for checking, whereas
the methods of [karr] are based on manipulation of matrices
that could be large.
Data Translation
Reusing an existing procedure may require that data be
translated into the form expected by that procedure;
we describe in [novak:tose92] some methods for semi-automatic
data translation. If a procedure requires that its data be presented
in particular units, then unit conversion may also be required.
The unit conversion methods of this paper can be
combined with the methods of [novak:tose92] to accomplish this.
Unit conversion may also be required in preparing data for transmission
to a remote site over a network, or for use in a remote procedure call.
IDL (Interface Description Language) [lamb87] allows
exchange of large structured data, possibly including structure
sharing, between separately written components of a large software
system such as a compiler. Use of IDL requires that the user write
precise specifications of the source and target data structures.
Herlihy and Liskov [herlihy] describe a method for transmission
of structured data over a network, with a possibly different data
representation at the destination. Their method employs user-written
procedures to encode and decode the data into transmissible
representations.
Unit Representation
We use the term simple unit to refer to any named unit for which
an appropriate conversion factor and dimension (as described
later) have been defined. Simple units include the base units
of a system of measurement, such as meter and kilogram,
named units such as horsepower that can be defined
in terms of other units, and the SI prefixes such as nano
that are used for scaling. Positive, nonzero numeric constants are
also allowed as simple units. In addition, common abbreviations may
be defined as synonyms for the actual units, e.g., kg
is defined as a synonym for kilogram. (Treating
abbreviations as synonyms, rather than giving them a conversion
factor and dimension and treating them as units, avoids the possibility
that slightly different numeric factors might be specified for the
same unit under different names.)
A composite unit is a product or quotient of units, and a
unit is either a simple unit or a composite unit. We represent
units in Lisp syntax, so that composite units are written within
parentheses, preceded by an operator that is * or /.
Thus, the syntax of units is as follows:
|
simple-unit | ::= | symbol number |
|
unit | ::= | simple-unit
composite-unit |
|
composite-unit | ::=
| (* unit_1 ... unit_n )
(/ unit_1 unit_2 ) |
|
|
We say that a unit is normalized if nested product and quotient
terms have been removed as far as possible, so that the unit will be
at most a quotient of two products. Clearly, any unit can be normalized;
algorithms for simplification of units are described later.
|
flat-unit | ::= | simple-unit
(* simple-unit_1 ... simple-unit_n ) |
|
normalized-unit | ::= | flat-unit
(/ flat-unit_1 flat-unit_2 ) |
|
|
Unit Conversion
A single numeric conversion factor is associated with each simple
unit. The conversion factor is the number by which a quantity
expressed in that unit must be multiplied in order to be expressed in
the equivalent unit in the standard system of units. We have chosen
as our standard the SI (Syst`eme International d'Unit'es)
system of units [nist330] [iso-standard] [abramowitz];
a different standard system could be chosen without affecting the
algorithms described here. Thus, the conversion factor for
meter is 1.0, while the conversion factor for foot is
0.3048 since 1 foot = 0.3048 meter. The conversion
factor for a numeric constant is just the constant itself.
The conversion factor for a product or quotient of units is,
respectively, the product or quotient of the factors for the component
units. Based on these definitions, it is easy to define a recursive
algorithm that computes the conversion factor for any unit, whether
simple or composite. This algorithm is shown in pseudo-code form in
Fig. 1. Assuming that the definitions of units are
acyclic, the algorithm is guaranteed to terminate and requires time
proportional to the size of the unit expression tree.
function factor (unit)
- if unit is a simple unit (number or symbol),
- if unit is a number, return unit;
- if unit is a synonym of unit', return
factor (unit');
- if unit has a predefined conversion factor f,
return f;
- else, error: unit is undefined.
- otherwise,
- if unit is a product, (* u_1 ... u_n ),
return
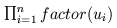
- if unit is a quotient, (/ u_1 u_2 ),
return factor( u_1 ) / factor( u_2 )
- else, error: unit has improper form.
Fig. 1: Conversion Factor Algorithm
Our system provides facilities for defining named simple units with
specified numeric conversion factors and for defining units in terms
of previously defined units. Examples of unit definitions are shown
in Fig. 2. In the first example, each unit is defined by
its name, numeric conversion factor, and a list of synonyms. In the
second example, the conversion factor is specified as an expression in
terms of previously defined units.
(defsimpleunits 'length
'((meter 1.0 (m meters))
(foot 0.3048 (ft feet))
(angstrom 1.0e-10 (a angstroms))
(parsec 3.083e16 (parsecs)) ) )
(defderivedunits 'force
'((newton
(/ (* kilogram meter) (* second second))
(nt newtons))
(pound-force
(/ (* slug foot) (* second second))
(lbf)) ) )
(ounce-force
(/ pound-force 16)
()) ) )
Fig. 2: Unit Definitions
We now consider conversion from a source unit, unit_s, to a
desired unit, unit_d. Let q_s be the numeric quantity
expressed in the source unit, q_SI be the equivalent quantity
in the standard (SI) system, and q_d be the quantity in the
desired unit. Let f_s = factor(unit_s) be the conversion
factor of the source unit and f_d = factor(unit_d) be the
conversion factor of the desired unit. Then we have the equations:
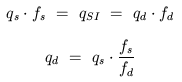
Thus, conversion to a desired unit is accomplished by multiplying
the source quantity by a factor f, where
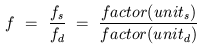
For example, to convert a measurement in terms of feet to
centimeters, the factor would be
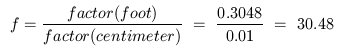
Given the factor algorithm shown in Fig. 1 that
computes the factor for any simple or composite unit, it is easy to
convert any combination of units to any equivalent combination. Since
a number is also defined as a unit, a numeric quantity of a given unit
can also be converted. The convert function takes as arguments
the source unit and desired unit; it returns the conversion factor
f, or NIL if the conversion is undefined or incorrect.
>(convert 'foot 'centimeter)
30.48
>(convert 'meters 'feet)
3.280839895013123
>(convert '(/ pi 6) 'degrees)
30.000000000005663
>(convert '(/ (* atto parsec)
(* micro fortnight))
'(/ inch sec))
1.0034552972545099
>(convert '(* acre foot) 'tablespoons)
8.3419459476381853E7
>(convert '(/ (* mega pound-force) acre)
'kilopascals)
1.0991794990738932
>(convert 'kilograms 'meters)
NIL
The last example, an attempt to make an incorrect conversion from
kilograms to meters, gives a result of NIL.
Dimensional analysis, as described in the next section, is used to
verify that a requested conversion is correct; if not, a result of
NIL is returned rather than a numeric conversion factor.
There are certain conversions that, while not strictly correct,
deserve a special note. The pound, for example, which is a
unit of mass, is often used as the name of the force unit that is
properly called pound-force. [The same confusion exists with
other mass units such as the ounce and the kilogram.] Conversion of
pounds to pounds-force involves an apparent conversion from mass to force.
Similarly, in particle physics the mass of a particle is often described using
energy units such as gigaelectronvolts (GeV). As described below,
the dimensional analysis system can either perform strict dimensional
checking and prohibit force-mass and energy-mass conversion, or it
can be made to detect and allow these specific conversions, with strict
checking otherwise. In the latter case, the following conversions are
allowed:
>(convert 'pound-force 'kilogram)
0.45359236999358599
>(convert '(* 1.67e-27 kg) 'gev)
0.93680115236643324
The conversion from mass units to the corresponding force units
requires multiplication by g, the conventional value for the
acceleration of free fall at the earth's surface (sometimes called
``gravity''), while the conversion from mass units to energy units
requires multiplication by the square of the speed of light. Each of
these is a physical constant, expressed in SI units.
Dimensional Analysis
If the above algorithms are to produce meaningful results, it must be
verified that the requested conversion is legitimate; it is clearly
impossible, for example, to convert kilograms to meters.
Correctness of unit conversion is verified by the long-established
technique of dimensional analysis [bridgman]: the source and
goal units must have the same dimensions.
Formally, we define a dimension as an 8-vector of integral powers
of eight base quantities. The base quantities are shown in Fig.
3 together with the base unit that is used for each quantity
in the SI system [nist330] [iso-standard]. We have added
money, which is not part of the SI system, as a dimension.
|
Index | Quantity | Unit |
|
0 | length | meter |
|
1 | time | second |
|
2 | temperature | kelvin |
|
3 | mass | kilogram |
|
4 | current | ampere |
|
5 | substance | mole |
|
6 | luminosity | candela |
|
7 | money | dollar |
|
|
Fig. 3: Base Quantities and Units
The dimension of a product of units is the vector sum of the
dimensions of its components, while the dimension of a quotient of
units is the vector difference of the dimensions of its components.
It can be verified that conversion from one unit to another is
legitimate by showing that the dimension vectors of the two units are
equal, or equivalently, that their difference is a zero vector.
The powers of base quantities that are encountered in
practice are usually small: they are seldom outside the range 4.
While a dimension can be represented as a vector of eight integer
values, with dimension checking done by operations on vectors,
this is somewhat expensive computationally. Since the integers in
the vector are small, it might be more efficient to pack them into bit
fields within an integer word. In this section, we describe a
variation of this packing technique. A dimension vector is encoded
within a single 32-bit integer, which we call a dimension integer,
using the algorithms presented below. Using this encoding, dimensions
can be added, subtracted, or compared using ordinary scalar integer
arithmetic.
It may be helpful to consider the analogy of doing vector arithmetic
by encoding vectors as decimal integers. For example, the vector
operation [1 2 3] + [2 2 4] = [3 4 7] can be simulated using
decimal integers: 123 + 224 = 347 . This technique will work as
long as it can be guaranteed that there will not be a ``carry'' from
one column of the decimal integer to another. We use a similar
method to encode a dimension vector as a 32-bit integer. A careful
justification of the conditions under which use of the integer encoding
is correct is presented following the algorithms. Finally, we argue
that these conditions will be satisfied in practice, so that use of the
integer encoding for dimension checking is justified.
We define two 8-vectors and an integer constant (shown in decimal
notation) as follows:
dimsizes = [20 20 20 10 10 10 10 10]
dimvals = [1 20 400 8000 80000
800000 8000000 80000000]
dimbias = 444444210
We assume for purposes of this presentation that the 8-vectors are
indexed beginning with 0; the index into an 8-vector for each
kind of quantity corresponds to the Index column shown in Fig.
3. The vector dimsizes gives the size of the field
assigned to each quantity; e.g., dimsizes[0] is 20,
corresponding to a field size of 20 and an allowable value range
of 9 for the power of length. The vector
dimvals gives multipliers that can be used to move a vector
value to its proper field position; it is defined as follows:
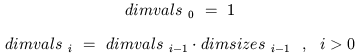
The integer dimbias is a value that, when added to a dimension
integer, will make it positive and will bias each vector component
within its field by half the size of the field. dimbias is
defined as:
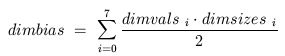
Given these definitions, algorithms are easily defined to convert
between an 8-vector form of dimension and the equivalent dimension
integer. A dimension integer is easily derived from a dimension
vector v as the vector dot product of v and
dimvals:
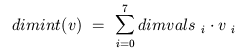
For example, the dimension integer for a force can be calculated as
follows:
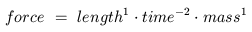
dimint( [ 1 -2 0 1 0 0 0 0 ] )
= (1 * 1) + (-2 * 20) + (0 * 400) + (1 * 8000)
= 7961
procedure dimvect (n, v)
integer m, sz, mm;
m := n + dimbias;
for i := 0 to 7 do
begin
sz := dimsizes[i];
mm := m / sz;
v[i] := (m - mm * sz) - sz / 2;
m := mm
end;
end;
Fig. 4: Conversion of Dimension Integer to Dimension Vector
A dimension integer can be converted back to an 8-vector by adding
dimbias to it and then extracting the values from each field.
This algorithm is not needed for unit conversion, but is provided
for completeness. The algorithm, shown in Fig. 4, has
as arguments a dimension integer n and an 8-vector v; it
stores the dimension values derived from n into v.
This procedure uses truncated division to extract the biased value
from each field of the integer encoding. The bias value, sz / 2,
is then removed to yield the signed field value. Dividing by the field
size is then used to bring the next field into the low-order position.
Our algorithm uses dimension integers, rather than dimension vectors,
to check the correctness of requested unit conversions. Addition,
subtraction, and comparison of dimension vectors are simulated by
scalar addition, subtraction, and comparison of corresponding
dimension integers. We can state the following theorems regarding
dimension integers:
Theorem 1:
If u and v are dimension vectors, then:
- dimint( u + v ) = dimint(u) + dimint(v)
- dimint( u - v ) = dimint(u) - dimint(v)
- dimint( - u ) = - dimint(u)
- if u = v , then dimint(u) = dimint(v)
These results follow immediately from the definition of dimint.
Theorem 2:
If u and v are dimension vectors, and dimint(u) = dimint(v),
and
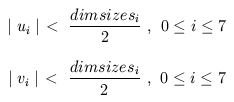
then u = v.
Proof: Suppose that dimint(u) = dimint(v) but u /= v.
Suppose that u_0 /= v_0. By the definition of dimint
and dimvals,
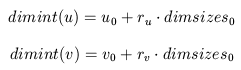
Since dimint(u) = dimint(v),
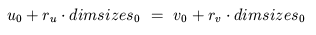
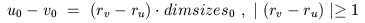
Therefore,
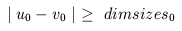
and by the triangle inequality, 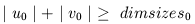 ,
but this is contrary to our assumptions that
,
but this is contrary to our assumptions that
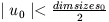 and
and 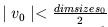 .
Therefore, it must be the case that u_0 = v_0 .
By inductive repetition of this argument on the remaining elements
of uand v, it must be the case that u = v .
Q.E.D.
.
Therefore, it must be the case that u_0 = v_0 .
By inductive repetition of this argument on the remaining elements
of uand v, it must be the case that u = v .
Q.E.D.
These theorems show that checking the dimensions of unit conversions
by means of dimension integers is correct so long as the individual
dimension quantities are less than half the field sizes given in the
dimsizes vector. We justify the use of the integer encoding of
dimension vectors as follows. The powers of dimension quantities that
are found in units that are used in practice are generally small --
usually within the range +/- 4. If a field size of 20 is assigned
to length, time, and temperature, and a field size of 10 is assigned
to the others, the dimension vector will fit within a 32-bit integer.
The representation allows a power of
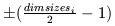
for each quantity. As long as each element of a dimension vector
is within this range, two dimension vectors are equal if and only if
their corresponding dimension integers are equal; furthermore, integer
addition and subtraction of dimension integers produce results equal
to the dimension integers of the vector sum and difference of the
corresponding dimension vectors. Our representation allows a power of
+/- 9 for length, time, and temperature, and a power of +/- 4
for mass, current, substance, luminosity, and money. This should be
quite adequate. We note that dimension vectors are used only in tests
of equality: unequal dimensions of source and goal units indicate an
incorrect conversion. An ``overflow'' from a field of the vector in
the integer representation will not cause an error to be indicated
when correct unit conversions are performed, because the two dimension
values will still be equal despite the overflow. Two unequal
dimension vectors will appear unequal, despite an overflow, unless the
incorrect dimension integer corresponds to a very different kind of
unit that has a dimension value that happens to be exactly equal; this
is most unlikely to happen accidentally. For example, if the user
attempts to convert a 20th power of length into a time, the system
will fail to detect an error. This is such an unlikely occurrence
that we consider the use of the more efficient integer encoding to be
justified. Note, however, that 8-vectors could be used for dimension
checking instead if desired.
Cunis [cunis92] describes an alternative representation of
dimensions. He represents dimensions as a rational number in Lisp,
i.e., as a ratio of integers that represent the positive and
negative powers of dimensions. Each base quantity, such as
length, is assigned a distinct small prime; the product of these,
raised to the appropriate powers, forms the integer used in the ratio.
This method requires somewhat more storage and computation than the
method we present, and arithmetic overflow could be a problem if
extended-precision arithmetic is not used; since Lisp provides
extended-precision integers, this is not a problem in Lisp.
Unit Conversion Checking
The dimension integer corresponding to a unit can be found as follows.
The dimension of a constant is 0; this is also the case for
units such as radian or nano. (Constants can be
considered to have a dimension of unity, whose logarithmic
representation is zero; such units are sometimes referred to as
``dimensionless'' [nist330].) The dimension of a base
quantity is given by the corresponding value in the vector
dimvals; for example, the dimension of time is dimvals[1]
or 20. The dimension integer of a product of units is the sum
of their dimension integers (using ordinary 32-bit integer
arithmetic), and the dimension of a quotient of units is the
difference of their dimensions. Dimensions of common abstract units
such as force are found by computing the dimension of their
expansion in terms of base abstract units; for force this
expansion is:
force = (/ (* mass length) (* time time))
We also define an abstract unit dimensionless with dimension
integer 0. When a unit symbol is defined to the system, its
dimension is determined from the abstract unit specified for it;
thus, in Fig. 2, meter receives the dimension of
length. When a unit is defined by an
expansion in terms of other units, the dimension of the expansion is
verified by comparison with the dimension of its abstract unit.
When convert is called to convert one unit to another, it
also computes the dimension of the source unit minus the dimension
of the goal unit. If the difference is 0, the dimensions are the
same, and the conversion is legitimate. A nonzero value indicates a
difference in dimensions of the source and goal units.
If strict conversion is desired, any difference in dimension is
treated as an error. In some cases, however, it may be desired to
allow automatic conversion between mass and force or between mass
and energy. Each of these conversions will produce a unique difference
signature, which can be recognized; the conversions and corresponding
dimension differences (source - goal) are shown in Fig. 5.
If the difference matches the integer signature, the conversion factor
should be multiplied by the additional factor shown in the table.
For example, in converting kilograms (mass) to newtons (force),
>(convert 'kilogram 'newton)
9.8066499999999994
the dimension of kilogram is 8000 and the dimension of
newton is 7961, so the difference is 8000 - 7961 = 39
and the proper multiplier is 9.80665. Although these multipliers
are expressed in SI units, the conversion works for all unit systems.
|
Conversion | Vector | Integer | Factor |
|
mass to weight | [ -1 2 0 0 0 0 0 0 ] | 39
| 9.80665 |
|
weight to mass | [ 1 -2 0 0 0 0 0 0 ] | -39
| 1 / 9.80665 |
|
mass to energy | [ -2 2 0 0 0 0 0 0 ] | 38
| 8.98755179E16 |
|
energy to mass | [ 2 -2 0 0 0 0 0 0 ] | -38
| 1 / 8.98755179E16 |
|
|
Fig. 5: Dimension Conversions
Units in Programming Languages
Although most modern programming languages require specification of
data types and feature compile-time type checking, units generally are
not included as part of types. This is unfortunate, since use of
incorrect units must be considered to be a type error. Some commonly
used procedures have implicit requirements on the units of their arguments;
for example, the system sin function may require that its
argument be expressed in floating-point radians. Karr and Loveman
[karr] advocated the inclusion of units in programming languages;
although the ATLAS language [atlas] incorporates units, to our
knowledge no widely-used programming language does so.
We have implemented the use of units in the GLISP language. GLISP
(``Generic Lisp'') [novak:glisp,novak:gluser] is a high-level
language with abstract data types that is compiled into Lisp (or into
C by an additional translation step); the GLISP compiler is
implemented in Common Lisp [steele-cltl]. GLISP has a data
description language that can describe Lisp data structures or data
structures in other languages. GLISP is described only briefly here;
for more detail, see [novak:tose92] and [novak:glisp].
In the sections below, we describe both the language features needed
to include units in a programming language and the compiler operations
necessary to perform unit checking and conversion.
Karr and Loveman [karr] suggested that units be implemented as
reserved words that could be used as multipliers in arithmetic
expressions. Instead, we have implemented units as part of data types.
The implementation of units within a programming language involves
several different aspects:
- inclusion of units as part of the type specification language
- type checking of uses of data that have units
- derivation of the units of the result of an arithmetic operation
- coercion of data into appropriate units when necessary
- a syntax for expressing numeric constants together with their units
Each of these aspects is described below.
Units as Part of Types
The types usually used to describe numeric data, such as integer,
real, etc., describe only the method of
encoding numeric values. The units denoted by the numeric values are
an independent issue. Therefore, both the numeric type and unit
must be specified as part of a data type. We have adopted a simple
syntax to specify the two together:
(units numeric-type unit )
For example, a floating-point number denoting a quantity of meters would
have the type:
(units real meters)
A type specification of this form may be used wherever a numeric type
specification such as real would otherwise be used.
Since the unit specification language allows constants to be included
as part of a unit, it is possible to specify unusual units
that might be used by hardware devices. For example, suppose that
an optical shaft encoder provides the angular position of a shaft
as an 8-bit integer, so that a circle is broken into 256 equal parts.
This unit can be expressed as:
(units integer (/ (* 2 pi radians) 256))
Results of Operations and Coercion
If unit checking and conversion are to be performed, it is necessary to
determine the unit of the result of an arithmetic operation.
In general, it is necessary to create and perhaps simplify new
symbolic unit descriptions. There are several classes of operations,
which are handled differently.
The units produced by multiplication and division are easily derived
by creating new units that symbolically multiply or divide, respectively,
the source units. For example, if a quantity whose unit is
(/ meter second) is multiplied by a quantity whose unit is
second, the resulting unit is:
(* (/ meter second) second)
This unit could be simplified to meter, but in most cases it is
not necessary for a compiler to perform such simplification:
usually only the numeric conversion factor and dimension of the unit
are used, and these are not affected by redundancy in the unit
specification.
Exponentiation to integer powers can be treated as multiplication or
division. The function sqrt is a special case: the dimension
vector of the argument unit must contain only multiples of 2, and it is
necessary to produce an output unit that is ``half'' the input unit;
this may require unit simplification, as discussed below.
There are differences of opinion regarding coercion of types by a
compiler. Some languages allow coercion within an arithmetic expression;
for example, if an integer and a real are added, the
integer will be converted to real prior to the addition.
Other languages allow coercion only across an assignment operator.
The most strict languages have no coercion and treat type differences
as errors. The same issues and arguments can be raised regarding
automatic coercion of units, and the same implementation
options are available. Note, however, that if no coercion is allowed,
the language must furnish some construct to allow the programmer to
invoke type conversion explicitly. We describe below
how automatic coercion can be implemented if it is desired.
In the case of addition, subtraction, comparison, and assignment
operations, the units of the two arguments must be the same if the
operation is to be meaningful. If the
units are unequal, an attempt is made to convert the unit of the
right-hand argument to the unit of the left-hand argument. If a
conversion factor fis not returned by the convert
algorithm, the operation is illegitimate (e.g., an attempt to
add kilograms to meters), and an error should be signaled
by the compiler.
(gldefun t1 (x: (units real meters)
y: (units real kilograms))
x + y)
glisp error detected by GLCOERCEUNITS in function T1
Cannot apply op + to METERS and KILOGRAMS
in expression: (X + Y)
If the conversion factor f is 1.0, no compiler action is
needed; this can occur if the units are equivalent but unsimplified.
If the conversion factor is other than 1.0, a multiplication of
the right-hand operand by the conversion factor must be inserted by
the compiler. The following example illustrates how the GLISP compiler
inserts such a conversion for an addition operation:
(gldefun t2 (x: (units real meters)
y: (units real feet))
x + y)
>(glcp 't2) ; compile function t2
result type: (UNITS REAL METERS)
(LAMBDA (X Y)
(+ X (* 0.30480000000000002 Y)))
In this example, the variable y, which has units feet, is
added to the value of the variable x, which has units meters.
In this case, the compiler has inserted a multiplication by the
appropriate factor to convert feet to meters prior to the addition.
The result type is the type of the left-hand argument; this convention
causes the type of a variable that is on the left-hand side of an
assignment statement to take precedence.
In some cases, it may be known that an argument of a procedure is
required to have certain units; in such cases, procedure arguments
can be type-checked and coerced if needed. For example, a library sin
function may require an argument in radians; if the unit of the
existing data is as described above for the shaft encoder example,
conversion will be required:
(gldefun t3 (x: (units integer (/ (* 2 pi radians)
256)))
(sin x))
result type: REAL
(LAMBDA (X)
(SIN (* 0.024543692606170259 X)))
We have not described any language mechanism to allow the programmer
to explicitly convert units to a desired form. Such a
conversion can be accomplished by assigning a value to a variable
that has the desired unit. The units used for intermediate results
within an arithmetic expression may be somewhat unusual, but will
always be converted to a programmer-specified unit upon assignment
to a variable. Conversion of units may generate extra multiplication
operations; however, if the compiler performs constant folding
[aho], these operations and their conversion factors can often be
combined with other constants.
Human programmers usually write programs in such a way that intermediate
results have reasonable units and reasonable numeric values.
When automatic coercion of units is performed,
it is possible that intermediate values may have unusual
units and very large or very small numeric values. It is possible that
compiler-generated unit conversions might cause a loss of accuracy
compared to code written by humans that does the unit conversions
explicitly. For this reason, it is advisable that automatic
coercion of units be used only with floating-point representations
with high accuracy, such as the 64-bit IEEE Standard representation.
While a human programmer who is aware of unit conversions can always
force the desired units to be used, a compiler that performs conversions
automatically might allow a careless programmer to overlook a potential
accuracy problem.
We have found that inclusion of units in programs tends to be ``all or
nothing''. That is, if units are specified for some variables, then
units need to be specified for other variables that appear in
expressions with those variables to avoid type errors.
Constants with Units
There may be a need to include physical constants, i.e., numbers
with attached units, as part of a program. We have adopted a syntax
that allows a numeric constant and unit to be packaged together:
'(q number unit )
The quoted q form indicates a quantity with units. The type of
the result is the type of the numeric constant combined with the
specified unit. For example, the speed of light could be written:
'(q 2.99792458e8 (/ meter second))
Unit Simplification
There are some cases in which unit simplification is needed.
For example, it is desirable to simplify a unit that describes the
result of a function. An algorithm for unit simplification should
be able to handle any combination of units, including mixtures of
units from different systems. The form of a unit that is considered to be
``simplified'' may depend on the needs of the user: an electrical engineer
might consider (* kilowatt hour) to be simplified, while a
physicist might prefer joule. We present below an algorithm
that works well in simplifying units for several commonly used
systems of units; in addition, it allows some customization by
specifying new unit systems.
A unit system is a set of base units that are by convention
taken as dimensionally independent, and a set of derived units,
formed from the base units by multiplication and division, that are
by convention used with the unit system. Other units that are used
for historical reasons may be associated with a unit system by defining
them in terms of a numeric conversion factor and a combination of
base units. We have implemented three unit systems: si
(the Syst`eme International or SI system), cgs
(centimeter-gram-second), and english (slug-foot-second). For
each commonly used kind of unit (e.g., length, force,
pressure, etc.) we define the standard unit for that kind of
unit in each system (e.g., meter, newton, and pascal,
respectively, for the si system).
Our algorithm for symbolic simplification of a unit is as follows:
- The desired system for the simplified result may be specified
as a parameter. If it is unspecified, the dominant system of the
input unit is determined by counting the number of occurrences of
units associated with known systems; if a dominant system cannot be
determined, si is used.
- The input unit is ``flattened'' so that it consists of a quotient
of two products. At the same time, input units are recursively expanded
to their equivalents in terms of base units (length, mass, time,
etc.). Units that are equivalent to numbers (have dimensionality
0), such as mega or degree, are converted to numbers.
- Any base units in the numerator and denominator product
lists that are not in the goal system are converted to the corresponding
units in the goal system. The conversion factors are accumulated.
- The numerator and denominator product lists are sorted
alphabetically.
- Corresponding duplicate units are removed from the lists
in a linear pass down the two lists; this cancels units that appear in
both numerator and denominator.
- The standard units that are defined for the goal system are
examined. If the multisets represented by the numerator and denominator
of the standard unit's expansion are contained in the numerator and
denominator, then the standard unit can be a factor of the simplified
unit. (The standard unit is also tested as an inverse factor.)
The largest standard unit factor (with size greater than one
base unit) is chosen, and it replaces its expansion
in the unit that is being simplified. This process is continued until
no further replacements can be made; it must terminate, since each
replacement makes the unit expansion smaller.
As an example, we show how the algorithm simplifies the unit expression:
>(simplifyunit '(/ joule watt))
The units joule and watt are defined in terms of base units:
joule = (/ (* KILOGRAM METER METER)
(* SECOND SECOND))
watt = (/ (* KILOGRAM METER METER)
(* SECOND SECOND SECOND))
The quotient of these two units is flattened as a quotient of two products:
(/ (* METER METER KILOGRAM SECOND SECOND SECOND)
(* SECOND SECOND METER METER KILOGRAM))
The two product lists are sorted:
(KILOGRAM METER METER SECOND SECOND SECOND)
(KILOGRAM METER METER SECOND SECOND)
Duplicated units in the two sorted lists are removed:
(SECOND)
()
In this case, the result is just a single unit: SECOND.
This algorithm has the advantage of being universal: by completely
breaking its input down to base units, canceling any duplicates,
and then making a new unit from the result, it can accept any combination
of units as input. It is also deterministic: it produces the same
result for any way of stating the same unit. The algorithm is also
reasonably fast. Since the algorithm works with a definition of a unit
system in terms of a set of preferred units, it is possible for a user
to define a modified unit system in which the user specifies the units
that are preferred as the result of simplification.
Some examples of unit simplification are shown below.
>(simplifyunit '(/ meter foot))
3.280839895013123
>(simplifyunit '(/ joule watt))
SECOND
>(simplifyunit '(/ joule horsepower))
(* 0.0013410220896139906 SECOND)
>(simplifyunit '(/ (* kilogram meter)
(* second second)))
NEWTON
>(simplifyunit 'atm)
(* 101325.0 PASCAL)
>(simplifyunit 'atm 'english)
(* 14.695948775721259 POUNDS-PER-SQUARE-INCH)
>(simplifyunit '(/ (* amp second) volt))
FARAD
>(simplifyunit '(/ (* newton meter)
(* ampere second)))
VOLT
>(simplifyunit '(/ (* volt volt)
(* lbf (/ (* atto parsec)
hour))))
(* 26250.801011041247 OHM)
It was mentioned above that determining the type returned by the sqrt
function requires making a unit that is ``half'' the input unit; for
example, if the input unit is (* meter meter), the output unit
would be meter. The process for determining the unit returned
by sqrt is the same as the process of unit simplification
described above, except for the last step. After the initial steps
of simplification, the input unit will be represented by flat, sorted
numerator and denominator lists containing base units of the
same unit system, and possibly a numeric factor. Both lists must
consist of adjacent pairs of identical units; otherwise, the input unit
is in error. The output unit is determined by collecting every other
member of the input lists (checking to make sure the alternate member
is identical) and making a new unit from these lists and the square
root of the numeric factor.
Units and Generic Procedures
We have done research on the reuse of generic procedures
[novak:kbse92] [novak:tose93]; a generic procedure is one
that can be used for a variety of data types. When the arguments of
a generic procedure include units, automatic checking and conversion
of units are essential for correct reuse.
In the GLISP language [novak:glisp] [novak:tose92], it is
not necessary to declare the type of every variable. When a variable
is assigned a value, type inference is used to determine the
type of the value, and the variable's type becomes the type of the
value assigned to it. (Assignment of values of different types to the
same variable will cause an error to be reported by the compiler.)
This feature is useful
in writing generic procedures: it is only necessary to specify the
main types that are used (often just the types of input parameters);
other types can be derived from those types. Because the types of
local variables are specified indirectly, a single generic procedure
can be specialized for a variety of input types. This is especially
useful in the case of types that include units.
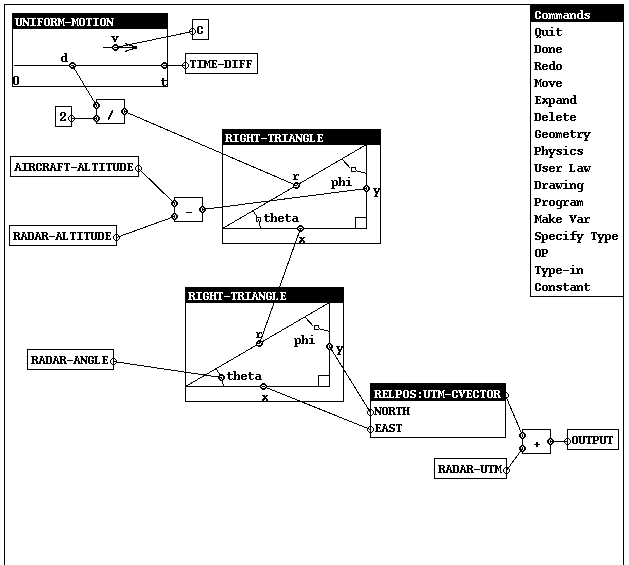
Fig. 6: VIP: Calculation of Position of Aircraft from Radar Data
We have developed a system, called VIP [novak:caia94] (for View
Interactive Programming) that generates programs from graphical
connections of physical and mathematical models. A program is generated
from equations associated with the physical models. Typically, only the
types and units of inputs and outputs are specified; the units and
types of intermediate values are derived by type and unit inference.
This system is illustrated in the diagram shown in Fig. 6.
The problem used as an example is a small but realistic numerical problem:
the calculation of the position of an aircraft from data provided by
an air search radar. We assume that the radar provides as input the
time difference between transmission and return of the radar pulse, as
well as the angle of the radar antenna at the time the return pulse is
detected. When the radar illuminates the aircraft, we assume that the
aircraft transponder transmits the identity of the aircraft and its
altitude. The position and altitude of the radar station are assumed
to be known. These items comprise the input data provided to the
program. We assume that the units of measurement of the input data
are externally specified (e.g., by hardware devices), so that the
program is required to use the given units.
In creating the program, the user of VIP is able to select from a
variety of predefined physical and mathematical models, constant
values, and operators. Initially, the VIP display consists of a set of
boxes representing the input data, and an output box. In our example,
the user first decides to model the travel of the radar beam as an
instance of uniform-motion. The user selects the Physics
command, then kinematics from the Physics menu, then
uniform-motion from the kinematics menu. The input value
TIME-DIFF is connected to the time button t of the motion.
Next, the user selects Constant and obtains the constant for the
speed of light, denoted C, and connects it to the velocity v
of the motion. The distance d of the motion then gives the total
(out-and-back) distance from the radar to the aircraft; by dividing this
distance by 2, the one-way distance is obtained. This distance
is connected to the hypotenuse of a Geometry object,
right-triangle. The difference between the altitude of the
aircraft and the altitude of the radar is connected to the y
of this triangle. The x of this triangle is then the distance to
a point on the ground directly underneath the aircraft. This distance
and the angle of the radar give a range and bearing to the aircraft from
the radar; by connecting these to another right triangle, x and
y offsets of the aircraft from the radar are obtained. These
are collected to form a relative position vector, RELPOS, which
is added to the radar's UTM (universal transverse mercator) coordinates
to form the output.
While the process described above is rather lengthy when described in
words, the time taken by an experienced user to create this program
using VIP was less than two minutes. Note that this problem involves
several instances of conversion of units of measurement, a physical
constant, and algebraic manipulation of several equations; all of
these were hidden and performed automatically. Fig. 7 shows
the GLISP program produced by VIP. Fig. 8 shows the program
after it has been compiled and mechanically translated into C.
(LAMBDA (TIME-DIFF: (UNITS INTEGER (* 100 NANOSECOND))
AIRCRAFT-ALTITUDE: (UNITS INTEGER (* 10 FOOT))
RADAR-ALTITUDE: (UNITS INTEGER (* 10 FOOT))
RADAR-ANGLE: (UNITS INTEGER (/ (* 2 PI RADIANS) 4096))
RADAR-UTM: UTM-CVECTOR)
(LET (OUT3 OUTPUT D2 OUT4 X3 Y2 X4 RELPOS:UTM-CVECTOR)
(OUT3 := (- AIRCRAFT-ALTITUDE RADAR-ALTITUDE))
(D2 := (* '(Q 2.997925E8 (/ M S)) TIME-DIFF))
(OUT4 := (/ D2 2))
(X3 := (SQRT (- (EXPT OUT4 2) (EXPT OUT3 2))))
(Y2 := (* X3 (SIN RADAR-ANGLE)))
(X4 := (* X3 (COS RADAR-ANGLE)))
(RELPOS := (A UTM-CVECTOR NORTH Y2 EAST X4))
(OUTPUT := (+ RELPOS RADAR-UTM))
OUTPUT))
Fig. 7: GLISP Program Generated by VIP for Radar Problem
CUTM *tqc (time_diff, aircraft_altitude, radar_altitude, radar_angle,
radar_utm)
long time_diff, aircraft_altitude, radar_altitude, radar_angle;
CUTM *radar_utm;
{
long out1;
CUTM *output;
float d1, out2, x1, y1, x2;
CUTM *relpos, *glvar1621;
out1 = aircraft_altitude - radar_altitude;
d1 = 2.997925E8 * time_diff;
out2 = d1 / 2;
x1 = sqrt(square(out2) - 9.2903039999999988E14 * lsquare(out1));
y1 = x1 * sin(0.0015339807878856412 * radar_angle);
x2 = x1 * cos(0.0015339807878856412 * radar_angle);
relpos = (CUTM*) malloc(sizeof(CUTM));
relpos->north = 1.0000000000000001E-7 * y1;
relpos->east = 1.0000000000000001E-7 * x2;
glvar1621 = (CUTM*) malloc(sizeof(CUTM));
glvar1621->east = relpos->east + radar_utm->east;
glvar1621->north = relpos->north + radar_utm->north;
output = glvar1621;
return output;
}
Fig. 8: Radar Program Compiled and Converted to C
In this example, unit conversion is a major part of the application
program. However, the user only needed to specify the input units;
all unit conversion and checking was performed automatically by the
compiler, so that this source of programming difficulty and potential
error was eliminated.
Conclusions and Future Work
We have described algorithms for conversion of units, for compiler
checking of units used in arithmetic operations and for coercing units
when necessary, and for symbolic simplification of combinations of units.
The unit conversion algorithms are as simple as possible: they require
only one multiply or divide per unit for conversion, and one add or
subtract per unit for dimension checking.
These algorithms have been implemented in a compiler that allows units
as part of data type specifications and that performs automatic unit
checking and conversion.
Unit conversion is a problem that will not go away, even if the
United States converts to the SI system. Workers in particular
fields will continue to use units such as parsec or micron
rather than meter, both because of tradition and because such
units are convenient in size for the measurements typically used
in practice. The compiler algorithms that we have described are
relatively easy to implement, so that units could be incorporated into
a variety of programming languages. These algorithms make it feasible
to implement essentially all known units of measurement, so that users
may use any units they find convenient. We agree with Karr and Loveman
[karr] that scientific programming languages should support the
use of units; we hope that presentation of these algorithms will
encourage such a trend.
The ARPA Knowledge-Sharing Project [neches91] focuses on
combining data from distributed databases and knowledge bases.
The algorithms described in this paper can be used for conversion when
these databases use different units.
We have included money as a dimension, since it is often
important to convert units such as (/ dollar kilowatt-hour)
that include monetary units. Of course, the conversion factors for
different currencies are not constant; however, by updating the
conversion factors periodically, useful approximate conversions can
be obtained.
Our algorithms do not handle units that include additive constants;
the common examples of such units are the Celsius and Fahrenheit
temperature scales. Other features of the GLISP language can be used
to handle these cases. Note that it is only possible to convert from
a pure temperature unit to another temperature unit; it would be
incorrect to multiply a non-absolute temperature by another unit.
The kelvin and the degree Rankine are linearly related and can be
converted by our algorithms.
Ruey-Juin Chang implemented an Analyst's Workbench [chang92] to
aid in making analytical models. She included substance as an
additional part of a quantity, along with numeric quantity and unit;
for example, ``10 gallons of gasoline'' has gasoline as the substance.
Engineering and scientific calculations often involve conversions
that depend on the substance as well as the quantity and units.
For example, ``10 gallons of gasoline'' can be converted into volume
(10 gallons), mass, weight, energy, money, or energy equivalent
in kilograms of anthracite coal. The algorithms presented in this
paper might usefully be extended to include these kinds of conversions
as well.
Software Available
The unit conversion software described in this paper is available
free by anonymous ftp from
ftp.cs.utexas.edu/pub/novak/units/ .
It is written in Common Lisp. An on-line demonstration of the software,
which requires a workstation running X windows, is available on the
World Wide Web via
http://www.cs.utexas.edu/users/novak .
Acknowledgements
Computer equipment used in this research was
furnished by Hewlett Packard and IBM.
I thank the anonymous reviewers for their suggestions for improving
this paper.
References
[abramowitz] M. Abramowitz and I. A. Segun, Handbook of
Mathematical Functions, National Bureau of Standards, 1964;
New York: Dover, 1968.
[ackley]
R. A. Ackley, Physical Measurements and the International (SI)
System of Units, San Diego, CA: Technical Publications, 1970.
[aho]
A. Aho, R. Sethi, and J. Ullman, Compilers:
Principles, Techniques, and Tools, Addison-Wesley, 1982.
[ansi-ieee-268]
American National Standard for Metric Practice,
ANSI/IEEE Standard 268-1992, 1992.
[atlas]
IEEE Standard C/ATLAS, IEEE Standard 716-1982.
[bridgman]
P. W. Bridgman, Dimensional Analysis, Yale Univ. Press, 1922.
[chang92]
R.-J. Chang, ``Cliche-Based Modeling for Expert
Problem-Solving Systems'', Ph.D. diss., C.S. Dept.,
Univ. Texas at Austin, 1992.
[cunis92]
R. Cunis, ``A Package for Handling Units of Measure in Lisp'',
ACM Lisp Pointers, vol. 5, no. 2, 1992.
[gruber-olsen94]
T. R. Gruber and G. R. Olsen, ``An Ontology for Engineering
Mathematics'', Proc. Fourth Int. Conf. on
Principles of Knowledge Representation and Reasoning,
San Mateo, CA: Morgan Kaufmann, 1994.
[gehani77]
N. Gehani, ``Units of Measure as a Data Attribute'',
Computing Languages vol. 2, no. 3, pp. 93-111, 1977.
[herlihy]
M. Herlihy and B. Liskov, ``A Value Transmission Method for
Abstract Data Types'', ACM Trans. Programming Languages
Syst., vol. 4, no. 4, pp. 527-551, Oct. 1982.
[hilfinger88]
P. N. Hilfinger, ``An Ada Package for Dimensional Analysis''.
ACM Trans. Programming Languages Syst., vol. 10,
no. 2, pp. 189-203, 1988.
[horvath]
A. L. Horvath, Conversion Tables of Units in Science and
Engineering, New York: Elsevier, 1986.
[iso-standard]
Quantities and Units, ISO Standards Handbook, 3rd ed.,
Geneva, Switzerland: International Organization for Standardization,
1993.
[karr]
M. Karr and D. B. Loveman, ``Incorporation of Units into
Programming Languages'', Communications of the ACM,
vol. 21, no. 5, pp. 385-391, May 1978.
[lamb87]
D. Lamb, ``IDL: Sharing Intermediate Representations'',
ACM Trans. Programming Languages Syst. vol. 9, no. 3,
pp. 267-318, July 1987.
[neches91]
R. Neches et al., ``Enabling Technology for Knowledge Sharing'',
AI Magazine, vol. 12, no. 3, pp. 36-56, Fall 1991.
[nist330] ``The International System of Units (SI)'',
National Inst. Standards Tech. Special Publication 330, Washington, DC:
Superintendent of Documents, U.S. Govt. Printing Office, 1991.
[novak:glisp]
G. Novak, ``GLISP: A LISP-Based Programming System With Data
Abstraction'', AI Magazine, vol. 4, no. 3, pp. 37-47, Fall 1983.
[novak:gluser]
G. Novak, ``GLISP User's Manual,'' Tech. Report STAN-CS-82-895,
C.S. Dept., Stanford Univ., 1982; TR-83-25, A.I. Lab, C.S. Dept.,
Univ. of Texas at Austin.
[novak:tose92]
G. Novak, F. Hill, M. Wan, and B. Sayrs, ``Negotiated Interfaces
for Software Reuse'', IEEE Trans. Software Engineering,
vol. 18, no. 7, pp. 646-653, July 1992.
[novak:kbse92]
G. Novak, ``Software Reuse through View Type Clusters'',
Proc. 7th Knowledge-Based Software Eng. Conf., IEEE Press,
Sept. 1992, pp. 70-79.
[novak:tose93]
G. Novak, ``Software Reuse by Specialization of Generic Procedures
through Views'', submitted for publication, 1994.
[novak:caia94]
G. Novak, ``Generating Programs from Connections of Physical Models'',
Proc. 10th Conf. on Artificial Intelligence for Applications,
IEEE Computer Society Press, March 1994, pp. 224-230.
[rossini]
F. D. Rossini, Fundamental Measures and Constants for
Science and Technology, Cleveland, OH: CRC Press, 1974.
[schulz]
C. A. Schulz, ``Writing Applications for Uniform Operation on a
Mainframe or PC: A Metric Conversion Program'', APL Quote Quad,
vol. 20, no. 4, pp. 348-361, ACM, July 1990.
[semioli]
W. J. Semioli and P. B. Schubert,, Conversion Tables for
SI Metrication, New York: Industrial Press, 1974.
[steele-cltl]
Steele, G., Common Lisp, Digital Press, 1990.
[wildi]
T. Wildi, Metric Units and Conversion Charts: A
Metrication Handbook for Engineers, Technologists, and Scientists,
2nd ed., Piscataway, NJ: IEEE Press, 1995.
Gordon S. Novak Jr.
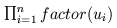
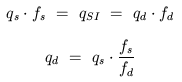
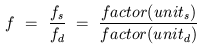
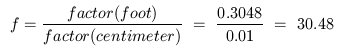
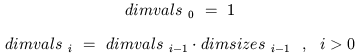
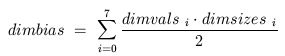
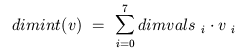
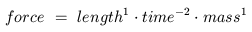
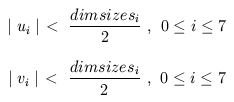
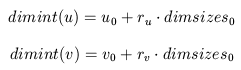
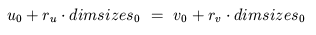
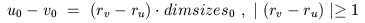
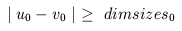
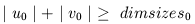 ,
but this is contrary to our assumptions that
,
but this is contrary to our assumptions that
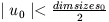 and
and 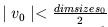 .
Therefore, it must be the case that u_0 = v_0 .
By inductive repetition of this argument on the remaining elements
of uand v, it must be the case that u = v .
Q.E.D.
.
Therefore, it must be the case that u_0 = v_0 .
By inductive repetition of this argument on the remaining elements
of uand v, it must be the case that u = v .
Q.E.D.