


Half Day Tutorial on
Using PLAPACK:
Parallel Linear Algebra Package
Submitted to SC98
Instructors
Greg Morrow
Robert van de Geijn
Department of Computer Sciences
and
Texas Institute for Computational and Applied Mathematics
The University of Texas at Austin
Austin, TX 78712
{morrow,rvdg}@cs.utexas.edu
Corresponding instructor:
Robert van de Geijn
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712
(512) 471-9720 (O)
(512) 471-8885 (F)
rvdg@cs.utexas.edu
http://www.cs.utexas.edu/users/rvdg
PLAPACK is a parallel (dense) linear algebra infrastructure designed
to correct problems with traditional approaches, including
-
Interface: Traditionally, libraries require linear systems be
distributed using a specific class of data distributions.
applications must manage communication required to build problems.
PLAPACK provides a convenient interface that hides communication
necessary to access matrices and vectors.
-
Distribution: Traditional approaches concentrate on the
distribution of matrices, and treat vectors as matrices of width one.
PLAPACK instead partitions vectors equally to all processors and
induces a matrix distribution from this vector distribution.
-
Abstraction: Traditional approaches code algorithms explicitly
exposing indices which often requires manual translation from global
indices to local indices. PLAPACK avoids this problem by using an
object-based (MPI-like) style, which hides indexing into individual
elements of matrices and vectors. This makes PLAPACK attractive both
for library development and education.
PLAPACK achieves these goals without sacrificing performance or
portability: PLAPACK Cholesky factorization attains more than 350
MFLOPS/processor on the Cray T3E-600 and has been ported to many
platforms.
Library users, library developers, and educators
Beginner - 25%
Intermediate - 50%
Advanced - 25%
The tutorial assumes that participants have familiarity with MPI and
basic dense linear algebra algorithms. While topics like the
application interface and new techniques for optimizing
parallel dense linear algebra algorithms should be of
interest to the ``high priests of high performance'',
these topics are presented at a level accessible to
beginners due to the simplicity of the PLAPACK interface.
Although not finalized, Intel has shown an interest
in providing a ``traveling Beowulf''
system for this tutorial, in form of a network of 8-16
Pentium based laptops connected with a fast switch.
As part of this tutorial, we will show how to
-
interface PLAPACK to an application, code in either FORTRAN or C,
-
implement high performance parallel dense linear algebra algorithms, and
-
customize existing code for special needs, using an example
from signal processing
In the introduction, we describe why traditional approaches
to parallel dense linear algebra libraries have fallen short.
We motivate a new philosophy, which places the application
(i.e. the vectors in a linear system) at the center of
the distribution of vectors and matrices to processors.
We show the benefits of encoding information about
vectors and matrices in opaque objects in an
MPI-like programming style. Finally, we motivate the
layering in the PLAPACK infrastructure, as presented
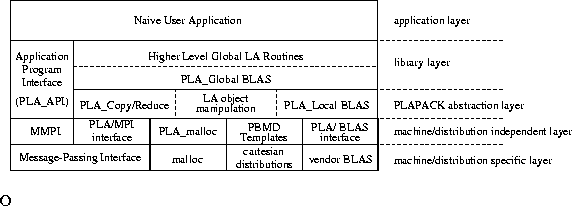
in Fig. 1.
Figure 1:
Layering of the PLAPACK infrastructure
 |
In this part of the tutorial, we show the participants how
to create and manipulate
distributed matrices and vectors,
how to fill them in an application-friendly fashion with
data, and how to call a simple PLAPACK library routine.
Finally, we show how to extract information from the
distributed matrices and vectors.
An example of a simple fill routine in given in
Fig. 2.
We will present the interface for both C and Fortran.
Upon completion of this part of the tutorial,
we will have developed an example code
that can be used to interface real applications with PLAPACK.
Figure 2:
Filling a global matrix by columns.
![\begin{figure}
\small
\listinginput[1]{1}{myfill.c}\end{figure}](img2.gif) |
In this part of the tutorial, we show how blocked
algorithms can be developed that achieve high performance using
Level-1, 2, and 3 Basic Linear Algebra Subprograms (BLAS).
Next, we show how to encode such algorithms using the PLAPACK
infrastructure, where each line of the resulting code
is a direct translation of the algorithm without the introduction
of indices or loop counters.
Let us illustrate this for the Cholesky factorization:
The Cholesky factorization of a square matrix A is given by
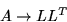
where A is symmetric positive definite and L is
lower triangular.
The algorithm for implementing this operation can be described
by partitioning the matrices

where A11 and L11 are 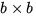 (b << n).
The
(b << n).
The 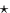 indicates the symmetric part of A.
Now,
indicates the symmetric part of A.
Now,
This in turn yields the equations
The above motivation yields an algorithm as it might appear
on a chalk board in a classroom, in Figure 3 (a).
In that figure, we take b = 1, so that A11 is a scalar and
A21 is a vector.
Since A is symmetric, only the lower triangular
part of the matrix is stored and
only the lower triangular part is updated.
The
PLAPACK implementation of the above described algorithm
is given in Figure 3 (b):
Figure 3:
Algorithm for computing the Cholesky factorization
of a matrix and its PLAPACK implementation
 |
All information that describes A, its data, and how it
is distributed to processors (nodes) is encoded in a
object (data-structure) referenced by a.
The PLA_Obj_view_all creates a second reference,
acur, into the same data.
The PLA_Obj_global_length call extracts the current
size of the matrix that acur currently references.
If this is zero, the recursion has completed.
The call to PLA_Obj_split_4 partitions the
matrix, creating new references for the four quadrants.
Element a11 is updated by taking its square root
in subroutine Take_sqrt, a21 is scaled by
1/a11 by calling PLA_Inv_scal, and
finally the symmetric rank-1 update is achieved
through the call to PLA_Syr. This sets up
the next iteration, which is also the next level of
recursion in our original algorithm.
In this part of the tutorial, we further develop the example
of the Cholesky factorization, showing how further optimizations
can be achieved by explicitly indicating duplication of data,
communicating without exposing actual communication calls,
and managing local communication. While this allows one to
achieve near-peak performance, still all indexing is hidden
from the user, as is communication.
In Fig. ![[*]](/icons/latex2html/icons.gif/cross_ref_motif.gif) , we show a number of such optimizations.
The final implementation presented is an algorithm which
would be very difficult to implement without the PLAPACK
infrastructure.
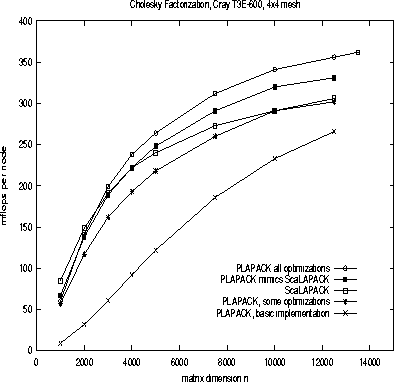
Representative performance is given in Fig. 5
, we show a number of such optimizations.
The final implementation presented is an algorithm which
would be very difficult to implement without the PLAPACK
infrastructure.
Representative performance is given in Fig. 5
Figure 4:
Various versions of level-3 BLAS based Cholesky factorization using
PLAPACK.
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3i...
...ormalsize (a) Blocked algorithm} \\ \hline\end{tabular}\end{center}\end{figure}](img8.gif) |
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3....
...b) Basic PLAPACK implementation} \\ \hline\end{tabular}\end{center}\end{figure}](img9.gif)
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3i...
...malsize (c) Basic optimizations} \\ \hline\end{tabular}\end{center}\end{figure}](img10.gif)
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3....
...{c}{\normalsize (d) New parallel algorithm}\end{tabular}\end{center}\end{figure}](img11.gif)
Figure 5:
Performance of the various algorithms
on a
16 processor configuration of the Cray T3E 600.
PLAPACK numbers are representative of the next release
of PLAPACK, while
ScaLAPACK numbers were measured using
Release 1.6.
All that should be concluded from these graphs is that
competitive performance can be attained, rather than that
one package outperforms the other, since it is natural
that they will leapfrog as new releases become available.
 |
While the previous part of the tutorial introduces
various techniques for optimizing PLAPACK implementations,
we now concentrate on the ease with which existing
implementations can be customized for a specific need.
To demonstrate this, we will derive a high performance
implementation of the QR factorization, and subsequently
show how by changing a few lines of the implementation,
it can be customized to perform ``updating'' of the
factorization. This customization makes the
QR factorization more appropriate for use in
signal processing when signals arrive incrementally
rather than being available a priori.
We conclude the tutorial by summarizing extensions of
PLAPACK that include MATLAB/Mathematica/HiQ/Labview
interfaces and use of PLAPACK for iterative methods.
See
http://www.cs.utexas.edu/users/plapack
-
PLAPACK Users' Guide:
Using PLAPACK: Parallel Linear Algebra Package, The MIT Press, Spring 1997.
An on-line version of this book is available via the PLAPACK
webpage.
-
We are developing an on-line tutorial from which materials will
be taken for this course.
This tutorial can be accessed via the PLAPACK webpage.
-
Robert van de Geijn is an Associate Professor of
Computer Sciences at the University of Texas at Austin. After obtaining a Ph.D. from the
University of Maryland, he joined
the University of Texas at Austin in 1987. He spend the 1990-91 academic
year at the University of Tennessee where he became involved in the
ScaLAPACK project.
His interests are in
Numerical Analysis, Parallel Numerical Algorithms and Parallel Communication
Algorithms.
-
Greg Morrow received his Ph.D. in Physics from The
University of Texas at Austin in Spring 1997.
Since then, he has been a postdoctoral research scientist in computer
sciences involved in the PLAPACK project.
His primary research interests include Stochastic and Quantum Chaos,
Parallel Numerical Algorithms, and Parallel Software Engineering.
-
Robert A. van de Geijn, Using PLAPACK, The MIT Press, 1997
-
Jack Dongarra, Robert van de Geijn and David Walker,
``Scalability Issues Affecting the Design of
a Dense Linear Algebra Library,''
Special Issue on Scalability
of Parallel Algorithms,
Journal of Parallel and Distributed Computing,
Vol. 22, No. 3, Sept. 1994.
-
Tom Cwik, Robert van de Geijn, and Jean Patterson,
``The Application of Parallel Computation
to Integral Equation Models of Electromagnetic Scattering,''
Journal of the Optical Society of America A,
Vol. 11, No. 4, pp. 1538-1545, April 1994
-
Jack Dongarra and Robert van de Geijn,
``Reduction to Condensed Form on Distributed Memory
Architectures,''
in Parallel Computing, 18, pp. 973-982, 1992.
-
Po Geng, J. Tinsley Oden, and Robert van de Geijn,
``Massively Parallel Computation for Acoustical Scattering
Problems using Boundary Element Methods,''
Journal of Sound and Vibration, 191 (1), pp. 145-165.
-
Almadena Chtchelkanova, John Gunnels, Greg Morrow, James Overfelt,
and Robert van de Geijn,
``Parallel Implementation of BLAS: General
Techniques for Level 3 BLAS,'' Concurrency: Practice and Experience to
appear.
-
Brian Grayson and Robert van de Geijn,
``A High Performance Parallel
Strassen Implementation,''
Parallel Processing Letters, Vol 6, No. 1 (1996) 3-12.
-
Robert van de Geijn and Jerrell Watts, ``SUMMA: Scalable Universal Matrix
Multiplication Algorithm,''
Concurrency: Practice and Experience, to
appear.
-
Greg Baker, John Gunnels, Greg Morrow, Beatrice Riviere, and
Robert van de Geijn,
``PLAPACK: High Performance through High Level Abstraction,''
Proceedings of ICPP98, to appear.
-
John Gunnels, Calvin Lin, Greg Morrow, and Robert van de Geijn, "A Flexible Class of Parallel Matrix Multiplication Algorithms",
Proceedings of IPPS98, 1998.
-
Philip Alpatov, Greg Baker, Carter Edwards, John Gunnels, Greg Morrow, James Overfelt, Robert van de Geijn, Yuan-Jye J. Wu,
"PLAPACK: Parallel Linear Algebra Package - Design Overview" ,
Proceedings of SC97, 1997.
-
Philip Alpatov, Greg Baker, Carter Edwards, John Gunnels, Greg Morrow, James Overfelt,
Robert van de Geijn, "PLAPACK: Parallel Linear Algebra Package," in Proceedings of the
SIAM Parallel Processing Conference, 1997.
-
Wu, Y.-J. J., A. A. Alpatov, C. Bischof, and R. A. van de Geijn, "A Parallel Implementation of
Symmetric Band Reduction Using PLAPACK", Proceedings of Scalable Parallel Library
Conference, Mississippi State. (October 1996, 8 pages, PRISM WN#35)
-
Ken Klimkowski and Robert van de Geijn, "Anatomy of an out-of-core
dense linear solver",
Proceedings of the 1995 International Conference on Parallel Processing,
pp. 29-33.
-
J. G. Lewis, D. G. Payne, and R. A. van de Geijn,
``Matrix-Vector Multiplication
and Conjugate Gradient Algorithms on Distributed
Memory Computers,''
Scalable High Performance Computing Conference 1994.
-
J. G. Lewis and R. A. van de Geijn,
``Implementing Matrix-Vector Multiplication
and Conjugate Gradient Algorithms on Distributed
Memory Multicomputers,''
Supercomputing '93.
-
James Demmel, Jack Dongarra, Robert van de Geijn and David Walker,
``LAPACK for
Distributed Memory Architectures:
The Next Generation,''
in Proceedings of the
Sixth SIAM Conference on Parallel Processing for Scientific
Computing, Norfolk, March 1993.
-
Jack Dongarra, Robert van de Geijn, and David Walker),
``A Look at Scalable Dense Linear Algebra Libraries,''
in Proceedings of Scalable High Performance Concurrent
Computing '92 (SHPCC92), April 27-29, 1992.
-
Anderson, E., Benzoni, A., Dongarra, J., Moulton, S., Ostrouchov, S.,
Tourancheau, B., and van de Geijn, R.,
``Basic Linear Algebra Communication Subprograms.''
in Sixth Distributed Memory Computing Conference Proceedings,
IEEE Computer Society Press, 1991, pp. 287-290.
-
Anderson, E., Benzoni, A., Dongarra, J., Moulton, S.,
Ostrouchov, S.,
Tourancheau, B., and van de Geijn, R.,
``LAPACK for Distributed Memory Architectures: Progress Report.''
in the Proceedings of the Fifth SIAM Conference on Parallel
Processing for Scientific Computing, SIAM, Philadelphia, 1992,
pp. 625-630.
G.W. Stewart
Department of Computer Science
University of Maryland
College Park, MD 20742
stewart@cs.umd.edu
Steven Huss-Lederman
Department of Computer Science
University of Wisconsin-Madison
1210 W. Dayton St.
Madison, WI 53706
lederman@cs.wisc.edu
Chris Bischof
Mathematics and Computer Science Division
Argonne National Laboratory
9700 S. Cass Ave.
Argonne, IL 60439
bischof@mcs.anl.gov
B.S. in Mathematics and Computer Science, University of
Wisconsin-Madison, Aug. 1981. Ph.D. in Applied Mathematics,
University of Maryland, College Park, Aug. 1987.
-
Associate Professor of Computer Sciences, UT-Austin, Sept. 1994 -
present.
-
Assistant Professor of Computer Sciences, UT-Austin, Sept. 1987 -
Aug. 1994.
-
Research Professor of Computer Sciences, Univ. of TN - Knoxville,
Aug. 1990 - May 1991
-
Dean's Fellow 1997-98 (Curriculum Development Award)
-
Faculty Fellowship #5 in Computer Sciences, (1995-present)
-
IBM Predoctoral Fellowship, 1986-87
- Ph.D. Students:
Mike Barnett (CS, 1992, with Chris Lengauer),
Timothy Collins (CS, 1995, with J.C. Browne),
Carter Edwards (CAM, 1997, with L. Hayes and M. Wheeler),
John Gunnels (CS, expected 1998),
James Overfelt (CAM, expected 1998)
-
Master's Students:
James Juszczak (CS, 1989),
Lance Shuler (Math, Fall 1992),
Martin Hoff (Math, 1993),
Kenneth Klimkowski (CAM, 1997)
-
Postdoctoral:
Greg Morrow,
Jurgen Singer,
Anna Elster
-
Robert A. van de Geijn, Using PLAPACK, The MIT Press, 1997
-
Jack Dongarra, Robert van de Geijn and David Walker,
``Scalability Issues Affecting the Design of
a Dense Linear Algebra Library,''
Special Issue on Scalability
of Parallel Algorithms,
Journal of Parallel and Distributed Computing,
Vol. 22, No. 3, Sept. 1994.
-
Tom Cwik, Robert van de Geijn, and Jean Patterson,
``The Application of Parallel Computation
to Integral Equation Models of Electromagnetic Scattering,''
Journal of the Optical Society of America A,
Vol. 11, No. 4, pp. 1538-1545, April 1994
-
Jack Dongarra and Robert van de Geijn,
``Reduction to Condensed Form on Distributed Memory
Architectures,''
in Parallel Computing, 18, pp. 973-982, 1992.
-
Po Geng, J. Tinsley Oden, and Robert van de Geijn,
``Massively Parallel Computation for Acoustical Scattering
Problems using Boundary Element Methods,''
Journal of Sound and Vibration, 191 (1), pp. 145-165.
-
Almadena Chtchelkanova, John Gunnels, Greg Morrow, James Overfelt,
and Robert van de Geijn,
``Parallel Implementation of BLAS: General
Techniques for Level 3 BLAS,'' Concurrency: Practice and Experience to
appear.
-
Brian Grayson and Robert van de Geijn,
``A High Performance Parallel
Strassen Implementation,''
Parallel Processing Letters, Vol 6, No. 1 (1996) 3-12.
-
Robert van de Geijn and Jerrell Watts, ``SUMMA: Scalable Universal Matrix
Multiplication Algorithm,''
Concurrency: Practice and Experience, to
appear.
-
Greg Baker, John Gunnels, Greg Morrow, Beatrice Riviere, and
Robert van de Geijn,
``PLAPACK: High Performance through High Level Abstraction,''
Proceedings of ICPP98, to appear.
-
John Gunnels, Calvin Lin, Greg Morrow, and Robert van de Geijn, "A Flexible Class of Parallel Matrix Multiplication Algorithms",
Proceedings of IPPS98, 1998.
-
Philip Alpatov, Greg Baker, Carter Edwards, John Gunnels, Greg Morrow, James Overfelt, Robert van de Geijn, Yuan-Jye J. Wu,
"PLAPACK: Parallel Linear Algebra Package - Design Overview" ,
Proceedings of SC97, 1997.
-
Philip Alpatov, Greg Baker, Carter Edwards, John Gunnels, Greg Morrow, James Overfelt,
Robert van de Geijn, "PLAPACK: Parallel Linear Algebra Package," in Proceedings of the
SIAM Parallel Processing Conference, 1997.
-
Wu, Y.-J. J., A. A. Alpatov, C. Bischof, and R. A. van de Geijn, "A Parallel Implementation of
Symmetric Band Reduction Using PLAPACK", Proceedings of Scalable Parallel Library
Conference, Mississippi State. (October 1996, 8 pages, PRISM WN#35)
-
Ken Klimkowski and Robert van de Geijn, "Anatomy of an out-of-core
dense linear solver",
Proceedings of the 1995 International Conference on Parallel Processing,
pp. 29-33.
-
J. G. Lewis, D. G. Payne, and R. A. van de Geijn,
``Matrix-Vector Multiplication
and Conjugate Gradient Algorithms on Distributed
Memory Computers,''
Scalable High Performance Computing Conference 1994.
-
J. G. Lewis and R. A. van de Geijn,
``Implementing Matrix-Vector Multiplication
and Conjugate Gradient Algorithms on Distributed
Memory Multicomputers,''
Supercomputing '93.
-
James Demmel, Jack Dongarra, Robert van de Geijn and David Walker,
``LAPACK for
Distributed Memory Architectures:
The Next Generation,''
in Proceedings of the
Sixth SIAM Conference on Parallel Processing for Scientific
Computing, Norfolk, March 1993.
-
Jack Dongarra, Robert van de Geijn, and David Walker),
``A Look at Scalable Dense Linear Algebra Libraries,''
in Proceedings of Scalable High Performance Concurrent
Computing '92 (SHPCC92), April 27-29, 1992.
-
Anderson, E., Benzoni, A., Dongarra, J., Moulton, S., Ostrouchov, S.,
Tourancheau, B., and van de Geijn, R.,
``Basic Linear Algebra Communication Subprograms.''
in Sixth Distributed Memory Computing Conference Proceedings,
IEEE Computer Society Press, 1991, pp. 287-290.
-
Anderson, E., Benzoni, A., Dongarra, J., Moulton, S.,
Ostrouchov, S.,
Tourancheau, B., and van de Geijn, R.,
``LAPACK for Distributed Memory Architectures: Progress Report.''
in the Proceedings of the Fifth SIAM Conference on Parallel
Processing for Scientific Computing, SIAM, Philadelphia, 1992,
pp. 625-630.
B.S. in Mathematics, Stanford University, June 1988.
Ph.D. in Physics, University of Texas at Austin, May 1997.
- Postdoctoral Fellow, Department of Computer Sciences and Texas Institute for
Computational and Applied Mathematics, University of Texas at Austin, May 1997-present.
- Software Engineering Coop, Intel Scalable Systems Division, Beaverton, Oregon,
1995-1996.
- Research Assistant, Departments of Physics and Computer Sciences, 1991-1995.
-
Almadena Chtchelkanova, John Gunnels, Greg Morrow, James Overfelt,
and Robert van de Geijn,
``Parallel Implementation of BLAS: General
Techniques for Level 3 BLAS,'' Concurrency: Practice and Experience to
appear.
-
Greg Baker, John Gunnels, Greg Morrow, Beatrice Riviere, and
Robert van de Geijn,
``PLAPACK: High Performance through High Level Abstraction,''
Proceedings of ICPP98, to appear.
-
John Gunnels, Calvin Lin, Greg Morrow, and Robert van de Geijn, "A Flexible Class of Parallel Matrix Multiplication Algorithms",
Proceedings of IPPS98, 1998.
-
Philip Alpatov, Greg Baker, Carter Edwards, John Gunnels, Greg Morrow, James Overfelt, Robert van de Geijn, Yuan-Jye J. Wu,
"PLAPACK: Parallel Linear Algebra Package - Design Overview" ,
Proceedings of SC97, 1997.
-
Philip Alpatov, Greg Baker, Carter Edwards, John Gunnels, Greg Morrow, James Overfelt,
Robert van de Geijn, "PLAPACK: Parallel Linear Algebra Package," in Proceedings of the
SIAM Parallel Processing Conference, 1997.
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -link 1 -show_section_numbers -address rvdg@cs.utexas.edu index.tex.
The translation was initiated by Robert van de Geijn on 5/26/1998



rvdg@cs.utexas.edu

![]()
![]()

![]() , we show a number of such optimizations.
The final implementation presented is an algorithm which
would be very difficult to implement without the PLAPACK
infrastructure.
Representative performance is given in Fig. 5
, we show a number of such optimizations.
The final implementation presented is an algorithm which
would be very difficult to implement without the PLAPACK
infrastructure.
Representative performance is given in Fig. 5
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3....
...b) Basic PLAPACK implementation} \\ \hline\end{tabular}\end{center}\end{figure}](img9.gif)
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3i...
...malsize (c) Basic optimizations} \\ \hline\end{tabular}\end{center}\end{figure}](img10.gif)
![\begin{figure}
\small
\begin{center}
\begin{tabular}
{c}
\begin{minipage}[t]
{3....
...{c}{\normalsize (d) New parallel algorithm}\end{tabular}\end{center}\end{figure}](img11.gif)
