Skip to main content

Section 2.2 Blocked Matrix-Matrix Multiplication

Unit 2.2.1 Basic Idea

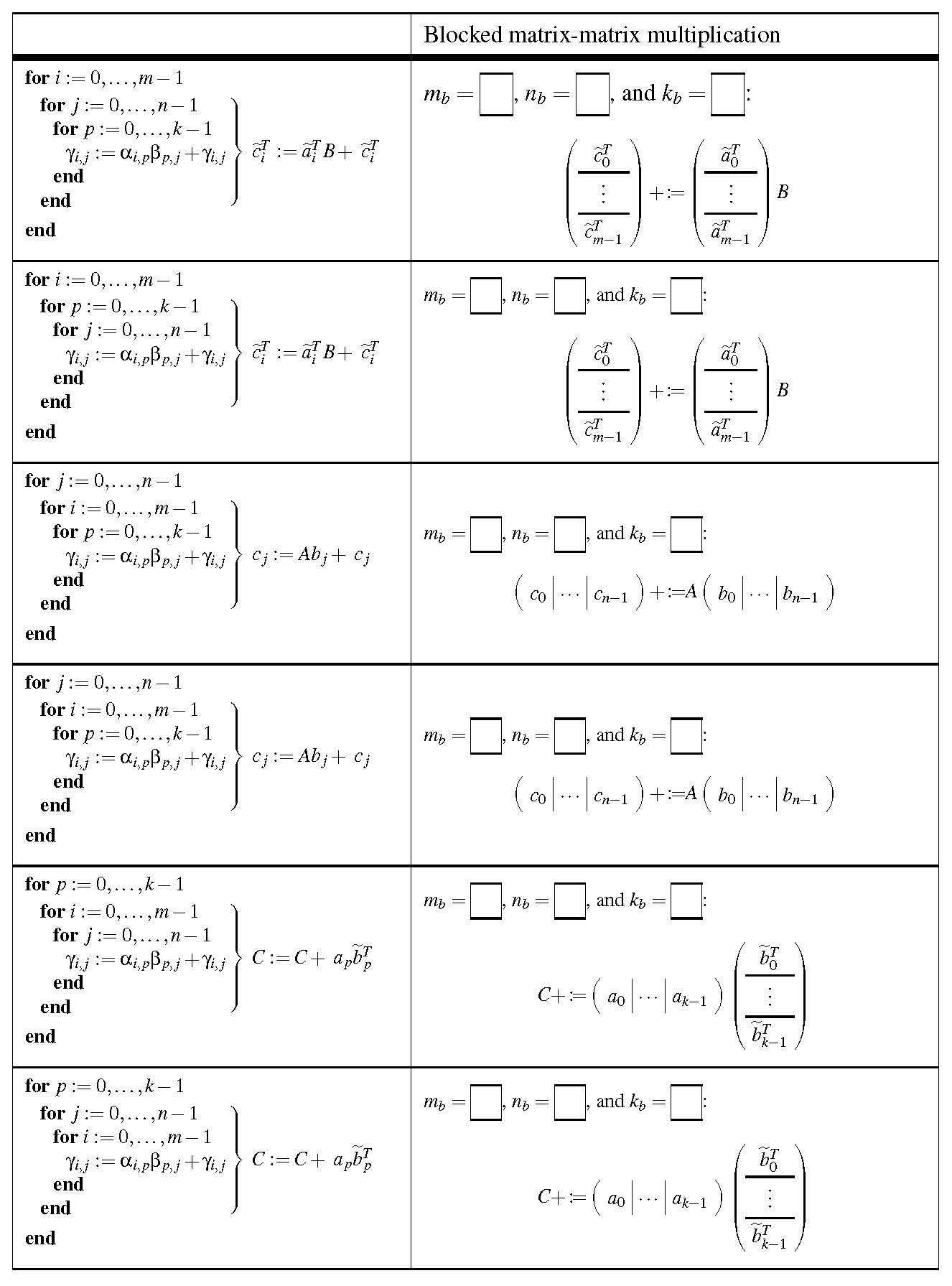
Key to understanding how we are going to optimize matrix-matrix multiplication is to understand blocked matrix-matrix multiplication (the multiplication of matrices that have been partitioned into submatrices).

Consider \(C := A B + C \text{.}\) In terms of the elements of the matrices, this means that each \(\gamma_{i,j} \) is computed by

\begin{equation*} \gamma_{i,j} := \sum_{p=0}^{k-1} \alpha_{i,p} \beta_{p,j} + \gamma_{i,j} . \end{equation*}

Now, partition the matrices into submatrices:

\begin{equation*} C = \left( \begin{array}{c | c | c | c } C_{0,0} \amp C_{0,1} \amp \cdots \amp C_{0,N-1} \\ \hline C_{1,0} \amp C_{1,1} \amp \cdots \amp C_{1,N-1} \\ \hline \vdots \amp \vdots \amp \amp \vdots \\ \hline C_{M-1,0} \amp C_{M-1,1} \amp \cdots \amp C_{M-1,N-1} \end{array} \right), \end{equation*}
\begin{equation*} A = \left( \begin{array}{c | c | c | c } A_{0,0} \amp A_{0,1} \amp \cdots \amp A_{0,K-1} \\ \hline A_{1,0} \amp A_{1,1} \amp \cdots \amp A_{1,K-1} \\ \hline \vdots \amp \vdots \amp \amp \vdots \\ \hline A_{M-1,0} \amp A_{M-1,1} \amp \cdots \amp A_{M-1,K-1} \end{array} \right), \end{equation*}

and

\begin{equation*} B = \left( \begin{array}{c | c | c | c } B_{0,0} \amp B_{0,1} \amp \cdots \amp B_{0,N-1} \\ \hline B_{1,0} \amp B_{1,1} \amp \cdots \amp B_{1,N-1} \\ \hline \vdots \amp \vdots \amp \amp \vdots \\ \hline B_{K-1,0} \amp B_{K-1,1} \amp \cdots \amp B_{K-1,N-1} \end{array} \right), \end{equation*}

where

  • \(C_{i,j} \) is \(m_i \times n_j \text{,}\)

  • \(A_{i,p} \) is \(m_i \times k_p \text{,}\) and

  • \(B_{p,j} \) is \(k_p \times n_j \)

with \(\sum_{i=0}^{M-1} m_i = m \text{,}\) \(\sum_{j=0}^{N-1} n_i = m \text{,}\) and \(\sum_{p=0}^{K-1} k_i = m \text{.}\) Then

\begin{equation*} C_{i,j} := \sum_{p=0}^{K-1} A_{i,p} B_{p,j} + C_{i,j} . \end{equation*}
Remark 2.2.2

In other words, provided the partitioning of the matrices is "conformal," matrix-matrix multiplication with partitioned matrices proceeds exactly as does matrix-matrix multiplication with the elements of the matrices except that the individual multiplications with the submatrices do not necessarily commute.

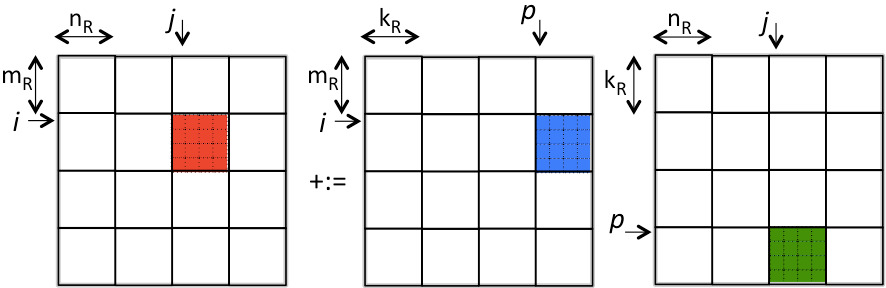
We illustrate how blocking \(C \) into \(m_b \times n_b\) submatrices, \(A \) into \(m_b \times n_b \) submatrices, and \(B \) into \(k_b \times n_b \) submatrices in Figure 2.2.3.

Figure 2.2.3 An illustration of a blocked algorithm where \(m_R = n_R = k_R = 4 \text{.}\)

An implementation of one such algorithm is given in Figure 2.2.4. 

void MyGemm( int m, int n, int k, double *A, int ldA,
	     double *B, int ldB, double *C, int ldC )
{
  for ( int j=0; j<n; j+=NB ){
    int jb = min( n-j, NB );    /* Size for "finge" block */ 
    for ( int i=0; i<m; i+=MB ){
      int ib = min( m-i, MB );    /* Size for "finge" block */ 
      for ( int p=0; p<k; p+=KB ){ 
        int pb = min( k-p, KB );    /* Size for "finge" block */ 
        Gemm_mbxnbxkb( ib, jb, pb, &alpha( i,p ), ldA, &beta( p,j ), ldB,
		                   &gamma( i,j ), ldC );
      }
    }
  }
}

void Gemm_mbxnbxkb( int m, int n, int k, double *A, int ldA, 
		    double *B, int ldB,  double *C, int ldC )
{
  for ( int p=0; p<k; p++ )
    for ( int j=0; j<n; j++ )
      for ( int i=0; i<m; i++ )
        gamma( i,j ) += alpha( i,p ) * beta( p,j );
}
Figure 2.2.4 Simple blocked algorithm that calls a kernel that updates a \(m_b \times n_b \) submatrix of \(C \) with the result of multiplying an \(m_b \times k_b \) submatrix of \(A \) times a \(k_b \times n_b \) submatrix of \(B \text{.}\)

Unit 2.2.2 Haven't we seen this before?

We already employed various cases of blocked matrix-matrix multiplication in Week 1.

In Section 1.3 we already used the blocking of matrices to cast matrix-matrix multiplications in terms of dot products and axpy operations. This is captured in

Figure 2.2.7 Click here to enlarge.

For each of partitionings in the right column, indicate how \(m_b \text{,}\) \(n_b \text{,}\) and \(k_b \) are chosen.

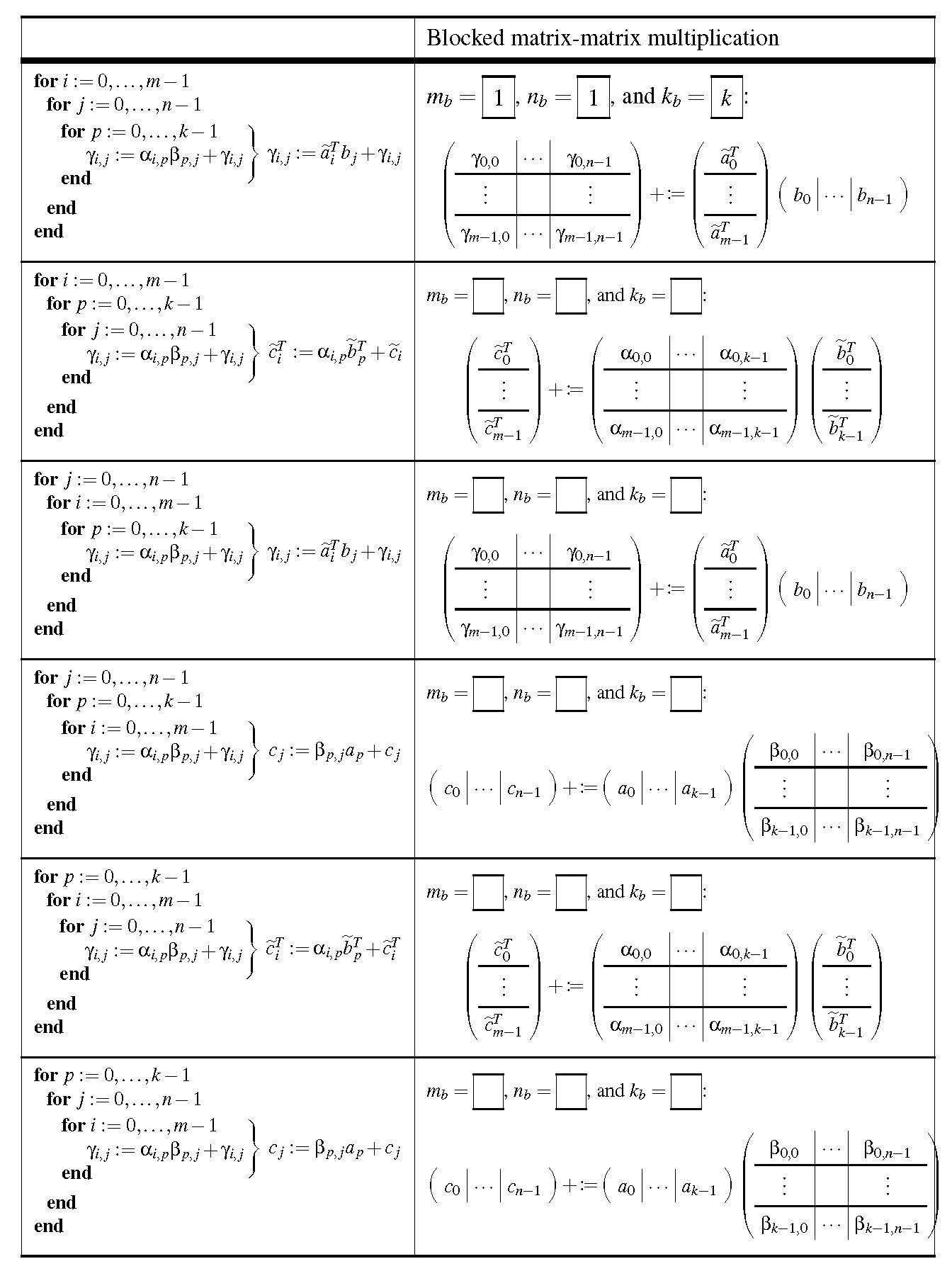
In Section 1.4, we already used the blocking of matrices to cast matrix-matrix multiplications in terms of matrix-vector multiplication and rank-1 updates. This is captured in

Figure 2.2.9 Click here to enlarge.

For each of partitionings in the right column, indicate how \(m_b \text{,}\) \(n_b \text{,}\) and \(k_b \) are chosen.