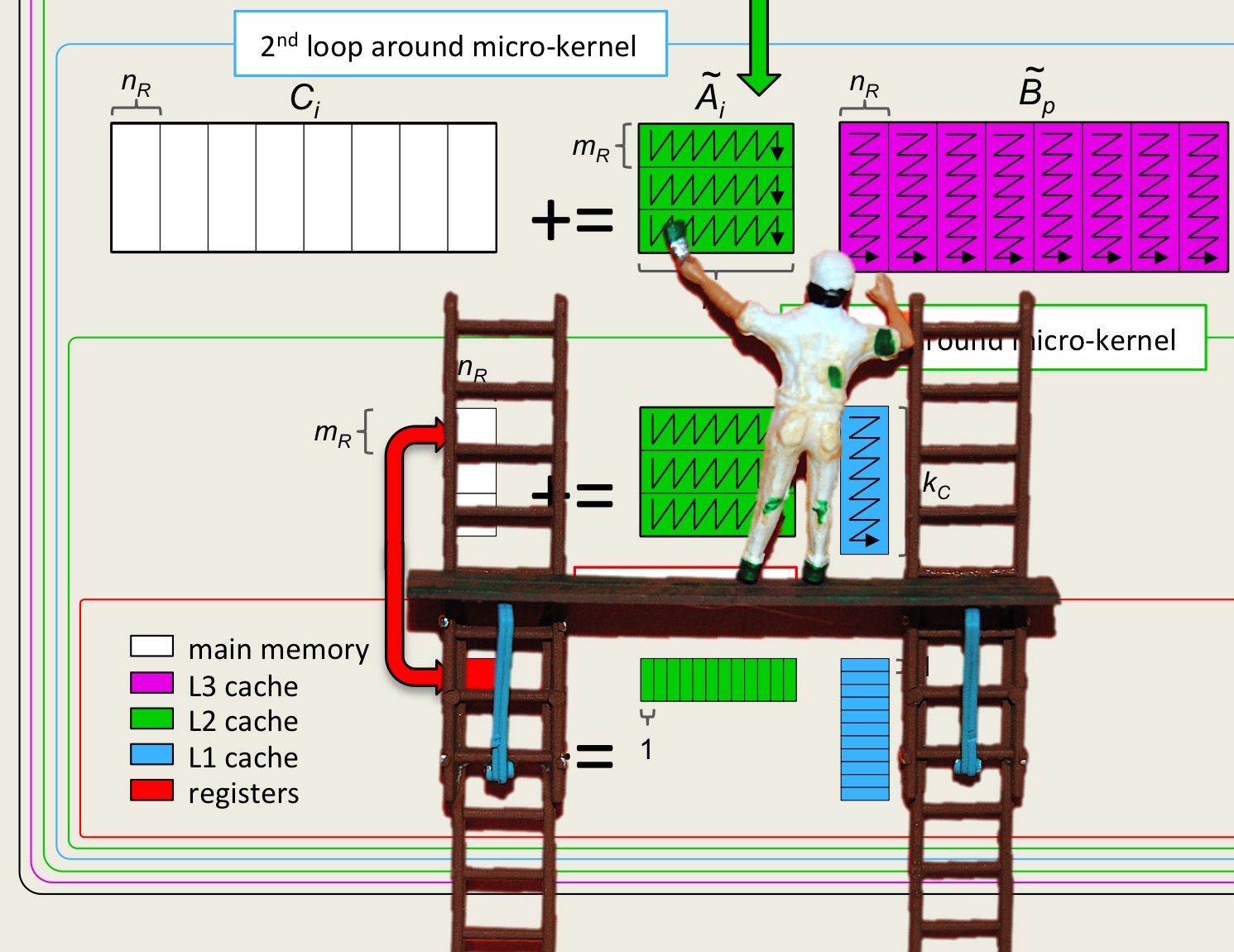
Unit 2.4.5 Optimally amortizing data movement
¶Homework 2.4.5.1.
In the discussion in the last unit, assume that a fixed number of elements in \(m_R \times n_R \) submatrix \(C_{i,j} \) can be stored in registers: \(m_R n_R = K \text{.}\) What choices of \(m_R \) and \(n_R \) maximize
the ratio of useful operations (floating point operations) to overhead (memory operations)?
Of course, our approach so far restricts \(m_R \) to be an integer multiple of the vector length, so that adds another contraint. Let's not worry about that.
You want to maximize
under the constraint that \(m_R n_R = K \text{.}\)
If you took a course in calculus, you may have been asked to maximize \(x y \) under the constraint that \(2( x+y) \) is constant. It might have been phrased as "You have a fixed amount of fencing to enclose a rectangular area. How should you pick the length, \(x \text{,}\) and width \(y \) of the rectangle?" If you think about it, the answer to this homework is closely related to this question about fencing.
Let's use \(x \) for \(m_R \) and \(y \) for \(n_R \text{.}\) We want to find \(x \) and \(y \) that maximize
under the constrant that \(x y = K \text{.}\) This is equivalent to finding \(x \) and \(y \) that minimize \(x + y \) under the constraint that \(x y = K \text{.}\)
Letting \(y = K / x \) we find that we need to minimize
By setting the derivative to zero, we find that the desired \(x \) must satisfy
Manipulating this yields
and hence \(x = \sqrt{K} \) and \(y = K / x = \sqrt{K} \text{.}\)
Strictly speaking, you should to check that it is a minimum of \(f(x)\) by examining the second derivative and checking that it is positive at the extremum.
Remark 2.4.7.
In practice, we have seen that the shape of the block of \(C\) kept in registers is not square for a number of reasons:
-
The formula for the number of vector registers that are used, when the vector length is four, is
\begin{equation*} \frac{m_R}{4} n_R + \frac{m_R}{4} + 1. \end{equation*}Even if the number of registers is a "nice number", it may not be optimal for \(m_R \) to equal \(n_R \text{.}\)
For now, \(m_R \) has to be a multiple of the vector length. Later we will see that we could instead choose \(n_R \) to be a multiple of the vector length. Regardless, this limits the choices.
The (load and) broadcast may be a more expensive operation than the load, on a per double that is loaded basis.
There are other issues that have to do with how instructions are pipelined that are discussed in a paper mentioned in Unit 2.5.1.