Unit 2.4.4 More options
¶You have now experienced the fact that modern architectures have vector registers and how to (somewhat) optimize the update of a \(4 \times 4 \) submatrix of \(C \) with vector instructions.
In the implementation in Unit 2.4.2, the block of \(C \) kept in registers is \(4 \times 4 \text{.}\) In general, the block is \(m_R \times n_R \text{.}\) If we assume we will use \(R_C \) registers for elements of the submatrix of \(C \text{,}\) what should \(m_R \) and \(n_R \) be to attain the best performance?
A big part of optimizing is to amortize the cost of moving data over useful computation. In other words, we want the ratio between the number of flops that are performed to the number of data that are moved between, for now, registers and memory to be high.
Let's recap: Partitioning
the algorithm we discovered in Section 2.3 is given by
We analyzed that its cost is given by
The ratio between flops and memory operations between the registers and memory is then
If \(k \) is large, then \(2 m n \) (the cost of loading and storing the \(m_R \times n_R \) submatrices of \(C \)) can be ignored in the denominator, yielding, approximately,
This is the ratio of floating point operations to memory operations that we want to be high.
If \(m_R = n_R = 4 \) then this ratio is \(4 \text{.}\) For every memory operation (read) of an element of \(A \) or \(B \text{,}\) approximately \(4 \) floating point operations are performed with data that resides in registers.
Homework 2.4.4.1.
Modify Assignments/Week2/C/Gemm_4x4Kernel.c to implement the case where \(m_R = 8 \) and \(n_R =
4 \text{,}\) storing the result in Gemm_8x4Kernel.c. You can test the result by executing
make JI_8x4Kernelin that directory. View the resulting performance by appropriately modifying
Assignments/Week2/C/data/Plot_optimize_MRxNR.mlx.
Homework 2.4.4.2.
Consider the implementation in Homework 2.4.4.1 with \(m_R \times n_R = 8 \times 4 \text{.}\)
How many vector registers are needed?
Ignoring the cost of loading the registers with the \(8 \times 4 \) submatrix of \(C \text{,}\) what is the ratio of flops to loads?
Number of registers:
Ratio:
Homework 2.4.4.3.
We have considered \(m_R \times n_R = 4 \times 4 \) and \(m_R \times n_R = 8 \times 4 \text{,}\) where elements of \(A \) are loaded without duplication into vector registers (and hence \(m_R \) must be a multiple of \(4 \)), and elements of \(B \) are loaded/broadcast. Extending this approach to loading \(A \) and \(B \text{,}\) complete the entries in the following table:
Remark 2.4.6.
Going forward, keep in mind that the cores of the architectures we target only have 16 vector registers that can store four doubles each.
Homework 2.4.4.4.
At this point, you have already implemented the following kernels: Gemm_4x4Kernel.c and Gemm_8x4Kernel.c. Implement as many of the more promising of the kernels you analyzed in the last homework as you like. Your implementations can be executed by typing
make JI_?x?Kernelwhere the ?'s are replaced with the obvious choices of \(m_R \) and \(n_R \text{.}\) The resulting performance can again be viewed with Live Script in
Assignments/Week2/C/data/Plot_optimize_MRxNR.mlx.
On Robert's laptop:
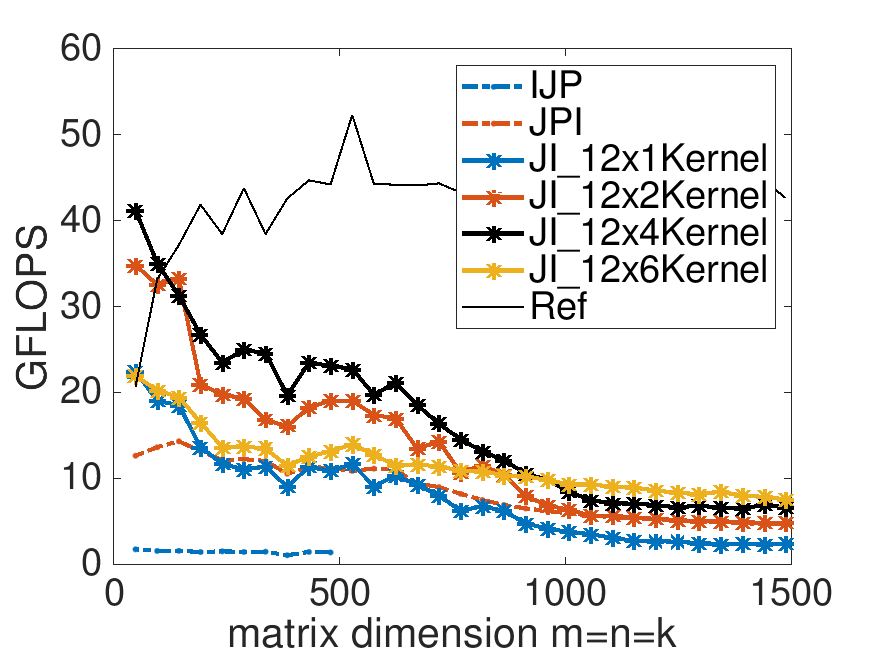
Performance of implementations for \(m_R = 4\) and various choices for \(n_R \text{:}\)

Performance of implementations for \(m_R = 8\) and various choices for \(n_R \text{:}\)
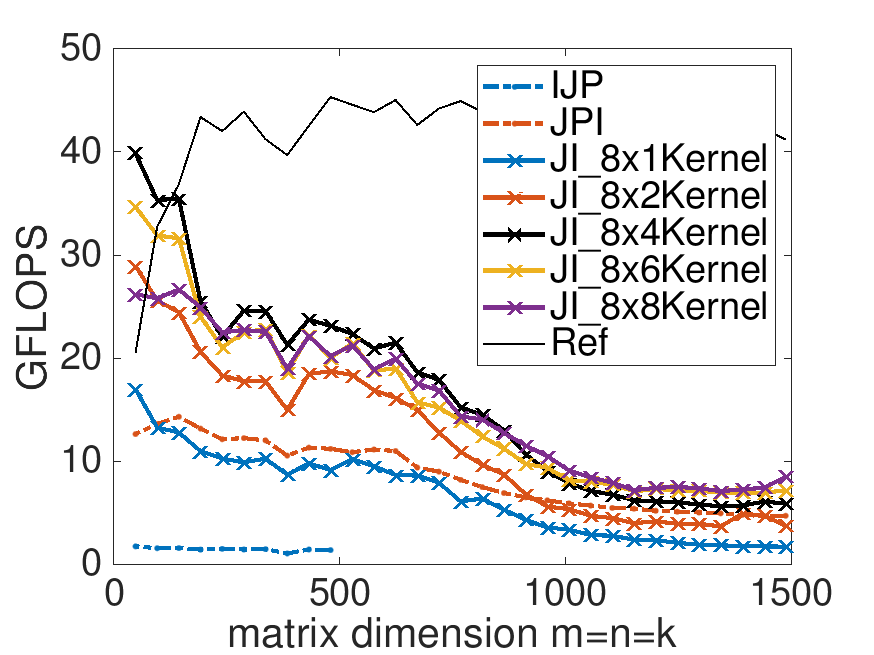
Performance of implementations for \(m_R = 12\) and various choices for \(n_R \text{:}\)