 , the equations may be
reduced to the single equation
, the equations may be
reduced to the single equation
In order to obtain some idea of the properties of the solution of
equations (27) the first approximation to them will be that of
linearisation. Absorbing the derivatives of the output functions
into the strengths of the connection matrices, and dropping the
input J and the lateral connection matrix  , the equations may be
reduced to the single equation
, the equations may be
reduced to the single equation
For the case that I is purely an initiator of activity, the growth of
 is exponential in time, with behaviour
is exponential in time, with behaviour
and so has time constant  , where a and b are the diagonal
elements of
, where a and b are the diagonal
elements of  and
and 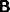 (when they are diagonal).
In the case
(when they are diagonal).
In the case  the
behaviour (29) will be of exponential increase, until the non-linearity
in the neuronal responses, especially that of saturation, becomes important.
For
the
behaviour (29) will be of exponential increase, until the non-linearity
in the neuronal responses, especially that of saturation, becomes important.
For  , the activity would initially be expected to die away.
In that case, it is necessary to take more careful account of the basal
ganglia contribution. Then, again in the diagonal case, and reducing to
the largest eigenvalue of
, the activity would initially be expected to die away.
In that case, it is necessary to take more careful account of the basal
ganglia contribution. Then, again in the diagonal case, and reducing to
the largest eigenvalue of  , for the behaviour of
, for the behaviour of  as
as
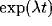 , there results the solution
, there results the solution
In the case that all of a, b, c and d are positive, which seems
supported by the neurobiology, then it is still possible to have
 in (30) even though
in (30) even though  . This is so for any value of
. This is so for any value of
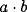 provided that
provided that 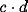 is large enough.
is large enough.
Given that it is always possible to have an increasing activity on the
frontal cortex, for suitably large basal ganglia to thalamus connection
weights, it is then possible to see that this activity will saturate
when the non-linear response function  in equation (27) is
used. To see this, it is only necessary to include the non-linearity
in equation (27) is
used. To see this, it is only necessary to include the non-linearity  of the thalamic output. Equation (27) then becomes
of the thalamic output. Equation (27) then becomes
The asymptotic value 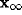 will therefore satisfy the
equation (dropping the external input
will therefore satisfy the
equation (dropping the external input  )
)
This has a bounded solution, for any connection matrix. The general form of the temporal development of the activities of the modules will thus, for large enough strength of connectivity from basal ganglia to thalamus (as noted above), be of an initial exponential rise of activity, followed by saturation for a period depending on the external input. If that latter acts in an inhibitory manner at a certain time value, then it is possible to see that this will cause the activity of equation (32) to die away. This would agree with the general form of the experimental activities shown, for example, on the left hand column of Figure 5 of Zipser [52].
The presence of more than one attractor is clear from the relation of (31)
to a BAM [24,30], to which it is identical when
 ,
,
 . More generally a number of attractors will be
expected, with noise causing transitions between them [25,53].
. More generally a number of attractors will be
expected, with noise causing transitions between them [25,53].
The training necessary to achieve such active memory behaviour is
obtainable through simple Hebbian learning on the basal ganglia
connection weights  and
and  , since as these increase they will
enable the lifetime of the neuronal activity of the cortical nodes to
increase, according to equation (30). This has already been investigated in
[49], to which the reader is referred.
, since as these increase they will
enable the lifetime of the neuronal activity of the cortical nodes to
increase, according to equation (30). This has already been investigated in
[49], to which the reader is referred.
An important feature of active memory is whether or not the ACTION net acts as a flip-flop for non-zero input. Thus the simplest ACTION net
in the limit that  is the Heaviside step function
is the Heaviside step function 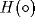 , is
turned on permanently by an input
, is
turned on permanently by an input 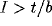 , but only transiently for
, but only transiently for  .
Replacing
.
Replacing  by a smooth sigmoid function in (33) will then lead to a
smoothly increasing and saturating response to a large enough input,
but a transient decaying response to a smaller one. The first of these
two possibilities are observed in the cells of Figure 1 of Zipser et al.
[53], and in the growing population vector in Figure 11 of
Georgopoulos et al. [20]; the latter is presented in Fuster [18].
by a smooth sigmoid function in (33) will then lead to a
smoothly increasing and saturating response to a large enough input,
but a transient decaying response to a smaller one. The first of these
two possibilities are observed in the cells of Figure 1 of Zipser et al.
[53], and in the growing population vector in Figure 11 of
Georgopoulos et al. [20]; the latter is presented in Fuster [18].
It is possible to model the growth of neuronal activity in the
Georgopoulos et al. results as follows. For N neurons, each with optimal
angular direction  for the i'th neuron, let that cell
have input
for the i'th neuron, let that cell
have input  arising from some directional input with
information that it involves the vector (angular) direction. For the linear
case, with t=0 in (32) (and diagonal connection matrices), the
asymptotic activity of each ACTION cortical neuron becomes
arising from some directional input with
information that it involves the vector (angular) direction. For the linear
case, with t=0 in (32) (and diagonal connection matrices), the
asymptotic activity of each ACTION cortical neuron becomes
(where it is assumed that 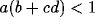 ). Then the population vector output
points along the desired direction, since this vector has value
). Then the population vector output
points along the desired direction, since this vector has value
where only 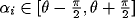 has been
used to have a positive output from
the neurons in (34), and the sum over random directions i in that interval
for the cross terms
has been
used to have a positive output from
the neurons in (34), and the sum over random directions i in that interval
for the cross terms  may be shown to be zero for large enough N.
The time constant to rise to saturation of about 200 msec [20]
would be expected to be obtainable for a suitable range of
connection weights and thresholds.
may be shown to be zero for large enough N.
The time constant to rise to saturation of about 200 msec [20]
would be expected to be obtainable for a suitable range of
connection weights and thresholds.