

Next: Long Range Connections
Up: The Role of Lateral
Previous: Dynamic Pattern Formation
We define the local field potential ( LFP) to be the total spiking
activity of all units within a circle of radius r around any
particular unit. In general, we use r=10, an area large enough to
include inhibitory interactions (which occur on a ring 8 and 9
lattice constants away). Our definition of the LFP is a crude
approximation of the signal recorded by low-pass filtering the
electrical signal from a low-impedance micro-electrode, and does
not include any dendritic or synaptic component. We will contrast this
with the spiking activity from a single unit (single-unit activity or
SUA).
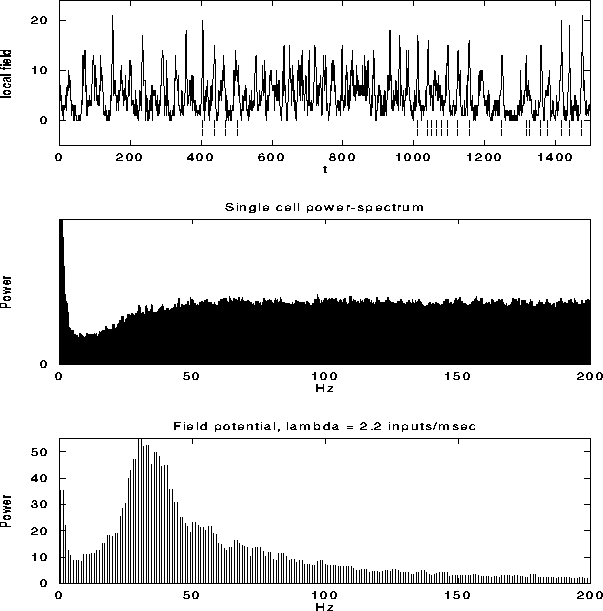
Figure 6:
The top graph shows the local field potential (LFP), computed
by summing the spiking activity of all leaky integrate-and-fire units
within a disk of radius r=9, as a function of time during a typical
simulation. We superimposed (dashed line) the spikes from a
representative unit in the same part of the network. The average
single unit activity (SUA) power spectrum (middle graph) shows such
peak and is typical of the spectrum of a Poisson process with
refractory period. The power spectrum of the LFP, shown in the bottom
panel, shows a clear peak around 30 Hz. Although not shown, the
variability in the interspike interval distribution is high, in
accordance with experimental data.
Fig. 6a shows the LFP during a typical simulation run.
The strongly fluctuating signal has a broad peak
(25-45 Hz) in the power spectrum (Fig. 6c). This
implies that the cells that contribute to the LFP are partially
synchronized (at most only about 25 out of the 400 cells fire
together), leading to broad oscillatory characteristics. The SUA tends
to be aligned with the maxima of the LFP, as reported experimentally,
without showing any significant evidence of periodic firing or a peak
in the associated single-cell power spectrum (Fig. 6b).
To test whether this behavior is a trivial outcome for any model of
spiking cells with feedback connectivity, we performed simulations
using the same neural model, except for one change: each cell had
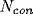 excitatory and
excitatory and 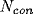 inhibitory synapses onto units
chosen at random (independent of distance) on the lattice. The
power spectra of the SUA and LFP are displayed in
Fig. 7. The single cell power spectrum now has a large
peak, implying that the discharge pattern of single cells is periodic.
Such power spectra are in general not found in spike trains of
non-bursting cells [4]. Furthermore, the interspike
interval variability under this condition is much lower than observed
experimentally [58] in cells firing
at medium or large rates. Because of the lack of spatial structure
the system is ergodic; that is the population average (the LFP in
Fig. 7) has essentially the same structure as the temporal
average over a single unit (the SUA in Fig. 7).
inhibitory synapses onto units
chosen at random (independent of distance) on the lattice. The
power spectra of the SUA and LFP are displayed in
Fig. 7. The single cell power spectrum now has a large
peak, implying that the discharge pattern of single cells is periodic.
Such power spectra are in general not found in spike trains of
non-bursting cells [4]. Furthermore, the interspike
interval variability under this condition is much lower than observed
experimentally [58] in cells firing
at medium or large rates. Because of the lack of spatial structure
the system is ergodic; that is the population average (the LFP in
Fig. 7) has essentially the same structure as the temporal
average over a single unit (the SUA in Fig. 7).
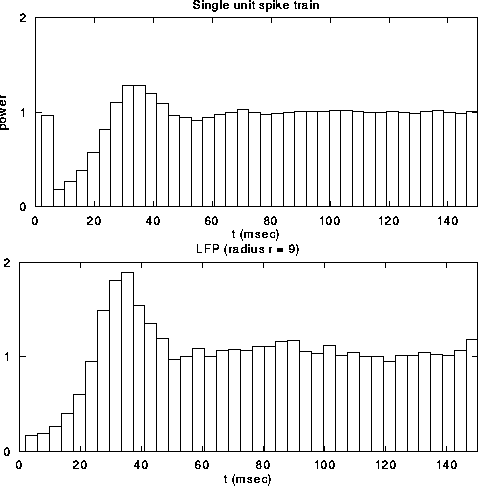
Figure 7:
The power spectrum of individual cells (upper panel) versus
the spectrum of the LFP (lower panel) in a network with non-local
random connectivity with both excitation and inhibition (everything
else is identical to the previous figure). Here, both signals display a
strong oscillatory component. The interspike interval variability is
much lower under these conditions than observed empirically.
The oscillations in the LFP depend most strongly on the amount of
lateral inhibition 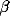 and the rate of external input
and the rate of external input 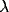 in
the model. Increasing
in
the model. Increasing 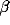 leads to a much sharper spectral peak
(especially for
leads to a much sharper spectral peak
(especially for 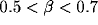 ) and to a small increase in the
location of the peak. Increasing the input rate
) and to a small increase in the
location of the peak. Increasing the input rate 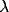 has a more
pronounced effect, leading simultaneously to broadening of the peak
and to an increase in the mean frequency.
has a more
pronounced effect, leading simultaneously to broadening of the peak
and to an increase in the mean frequency.
The large, broadly periodic fluctuations in the LFP reflect partial
synchronized and correlated discharge patterns of cells in a local
population. We can explain the properties of the local field signal by
reducing it to correlations of its constituents. Since we define the
LFP to be the sum of all N single-unit spiking activity within a
circle of radius r, the auto-correlation function of the LFP will be
the sum of N auto-correlations functions 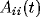 of the
individual cells and
of the
individual cells and 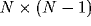 cross-correlation functions
cross-correlation functions
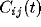 among individual cells within the circle,
among individual cells within the circle,
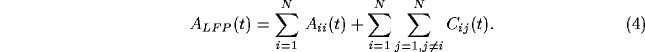
In general, the auto-correlation of the LFP will be dominated by the
cross-correlation functions among individual units and the power
spectrum of the LFP---identical to the Fourier transform of the
correlation function (Wiener-Khintchine theorem)---will in turn be
dominated by the sum of the Fourier transforms of the individual
cross-correlation functions. In order to characterize the power
spectrum of the LFP, we will now describe the characteristics of the
cross-correlations and their Fourier transforms.
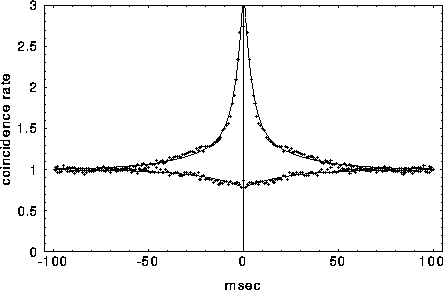
Figure 8:
Typical cross-correlation functions between neighboring
pairs of mutually excitatory cells (top graph) and mutually inhibitory
pairs separated by 9 lattice units. The solid lines indicate the best
least square fit of eq. 3 to the data, with the fast initial decay
(the ``tower") in 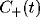 fitted by an exponential with
fitted by an exponential with
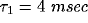 and the slower decay in both
and the slower decay in both 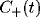 and
and 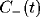 fitted by another exponential with
fitted by another exponential with 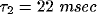 .
.
For mutually excitatory pairs of cells, the cross-correlation terms
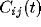 display a structure called a ``castle on a hill" in the
neurophysiological literature [33], i.e., a 10
to 20 msec wide peak centered at zero (Fig. 8) followed by
a slower decay to the asymptotic level of chance coincidences for long
time lags. The peak of
display a structure called a ``castle on a hill" in the
neurophysiological literature [33], i.e., a 10
to 20 msec wide peak centered at zero (Fig. 8) followed by
a slower decay to the asymptotic level of chance coincidences for long
time lags. The peak of 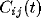 is always around zero and is
generated by recurrent excitation. At higher values of inhibition
is always around zero and is
generated by recurrent excitation. At higher values of inhibition
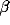 , a small but significant secondary peak in the cross-
correlation appears between the ``castle" and the slower decline. For
cell pairs that are 8 or 9 units distant, the interaction will be (on
average) mutually inhibitory and the associated correlation function
is characterized by a gentle trough that rises slowly to the
background level of chance coincidences at longer times. As discussed
in Usher et al. (1994), the process governing the slow decay in
the excitatory and the slow rise in the inhibitory correlation
functions is the same.
, a small but significant secondary peak in the cross-
correlation appears between the ``castle" and the slower decline. For
cell pairs that are 8 or 9 units distant, the interaction will be (on
average) mutually inhibitory and the associated correlation function
is characterized by a gentle trough that rises slowly to the
background level of chance coincidences at longer times. As discussed
in Usher et al. (1994), the process governing the slow decay in
the excitatory and the slow rise in the inhibitory correlation
functions is the same.
The principal factor leading to a power spectrum peak in the 30-70 Hz
range is the relative width of the excitatory cross-correlation peaks
to the inhibitory troughs. In general, the excitatory "castles" are
sharp relative to the broad dip in the cross-correlation due to
inhibition. In Fourier space, these relationships are reversed:
broader Fourier transforms of excitatory cross-correlations are paired
with narrower Fourier transforms of inhibitory
cross-correlations. Superposition of such transforms leads to a peak
in the 30-50 Hz range. A less important factor is the existence (at
higher values of inhibition) of a secondary peak around 20-30 msec in
the excitatory cross- correlations.
The principle behind the formation of the power spectrum peak can be
captured in the following simplified but generic example, which
assumes that the excitatory and inhibitory correlation functions
qualitatively behave as:
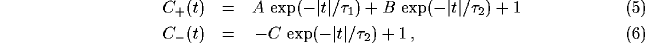
where the baseline of coincidence is normalized to 1. In
Fig. 8, we fitted these equations against two particular
cross-correlation functions from our network using 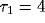 and
and
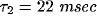 .
.
The power spectrum of the LFP, 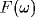 , will be dominated by the
Fourier transforms of many such correlation functions, with
, will be dominated by the
Fourier transforms of many such correlation functions, with

for 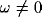 . The terms a and b account for the strength and
the number of excitatory and inhibitory cell pairs within the circle
(with
. The terms a and b account for the strength and
the number of excitatory and inhibitory cell pairs within the circle
(with 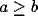 ).
).
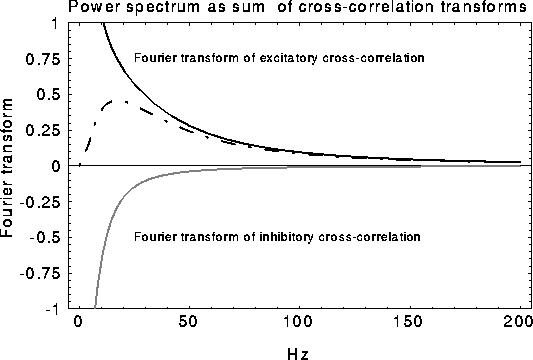
Figure 9:
Schematic of how the oscillatory peak in the LFP can be
caused by a sharply tuned excitatory cross-correlation function
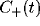 superimposed onto a much broader inhibitory cross-correlation
function
superimposed onto a much broader inhibitory cross-correlation
function 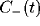 . If the two are subtracted, the low frequency
components cancel, leaving a peak at a non-zero frequency.
. If the two are subtracted, the low frequency
components cancel, leaving a peak at a non-zero frequency.
Consider now the simple case of 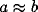 , which will occur in our
scenario if the LFP is taken over a circle with r > 9. In this case
the spectrum increases from low frequencies, reaches a maximum at
, which will occur in our
scenario if the LFP is taken over a circle with r > 9. In this case
the spectrum increases from low frequencies, reaches a maximum at
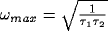 , and decays back to
zero for large frequencies. The superposition of two representative
cross-correlation transforms yielding the desired peak is shown in
Fig. 9).
, and decays back to
zero for large frequencies. The superposition of two representative
cross-correlation transforms yielding the desired peak is shown in
Fig. 9).


Next: Long Range Connections
Up: The Role of Lateral
Previous: Dynamic Pattern Formation

 excitatory and
excitatory and 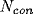 inhibitory synapses onto units
chosen at random (independent of distance) on the lattice. The
power spectra of the SUA and LFP are displayed in
Fig.
inhibitory synapses onto units
chosen at random (independent of distance) on the lattice. The
power spectra of the SUA and LFP are displayed in
Fig. 
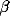 and the rate of external input
and the rate of external input 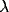 in
the model. Increasing
in
the model. Increasing 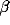 leads to a much sharper spectral peak
(especially for
leads to a much sharper spectral peak
(especially for 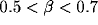 ) and to a small increase in the
location of the peak. Increasing the input rate
) and to a small increase in the
location of the peak. Increasing the input rate 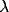 has a more
pronounced effect, leading simultaneously to broadening of the peak
and to an increase in the mean frequency.
has a more
pronounced effect, leading simultaneously to broadening of the peak
and to an increase in the mean frequency.
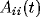 of the
individual cells and
of the
individual cells and 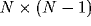 cross-correlation functions
cross-correlation functions
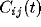 among individual cells within the circle,
among individual cells within the circle,
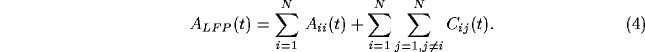

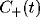 fitted by an exponential with
fitted by an exponential with
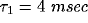 and the slower decay in both
and the slower decay in both 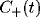 and
and 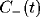 fitted by another exponential with
fitted by another exponential with 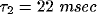 .
. 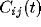 display a structure called a ``castle on a hill" in the
neurophysiological literature [
display a structure called a ``castle on a hill" in the
neurophysiological literature [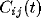 is always around zero and is
generated by recurrent excitation. At higher values of inhibition
is always around zero and is
generated by recurrent excitation. At higher values of inhibition
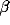 , a small but significant secondary peak in the cross-
correlation appears between the ``castle" and the slower decline. For
cell pairs that are 8 or 9 units distant, the interaction will be (on
average) mutually inhibitory and the associated correlation function
is characterized by a gentle trough that rises slowly to the
background level of chance coincidences at longer times. As discussed
in Usher et al. (1994), the process governing the slow decay in
the excitatory and the slow rise in the inhibitory correlation
functions is the same.
, a small but significant secondary peak in the cross-
correlation appears between the ``castle" and the slower decline. For
cell pairs that are 8 or 9 units distant, the interaction will be (on
average) mutually inhibitory and the associated correlation function
is characterized by a gentle trough that rises slowly to the
background level of chance coincidences at longer times. As discussed
in Usher et al. (1994), the process governing the slow decay in
the excitatory and the slow rise in the inhibitory correlation
functions is the same.
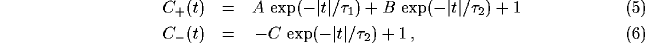
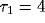 and
and
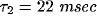 .
.
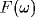 , will be dominated by the
Fourier transforms of many such correlation functions, with
, will be dominated by the
Fourier transforms of many such correlation functions, with

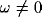 . The terms a and b account for the strength and
the number of excitatory and inhibitory cell pairs within the circle
(with
. The terms a and b account for the strength and
the number of excitatory and inhibitory cell pairs within the circle
(with 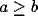 ).
).

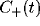 superimposed onto a much broader inhibitory cross-correlation
function
superimposed onto a much broader inhibitory cross-correlation
function 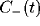 . If the two are subtracted, the low frequency
components cancel, leaving a peak at a non-zero frequency.
. If the two are subtracted, the low frequency
components cancel, leaving a peak at a non-zero frequency. 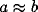 , which will occur in our
scenario if the LFP is taken over a circle with r > 9. In this case
the spectrum increases from low frequencies, reaches a maximum at
, which will occur in our
scenario if the LFP is taken over a circle with r > 9. In this case
the spectrum increases from low frequencies, reaches a maximum at
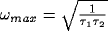 , and decays back to
zero for large frequencies. The superposition of two representative
cross-correlation transforms yielding the desired peak is shown in
Fig.
, and decays back to
zero for large frequencies. The superposition of two representative
cross-correlation transforms yielding the desired peak is shown in
Fig.