Unit 3.2.6 Translating into code
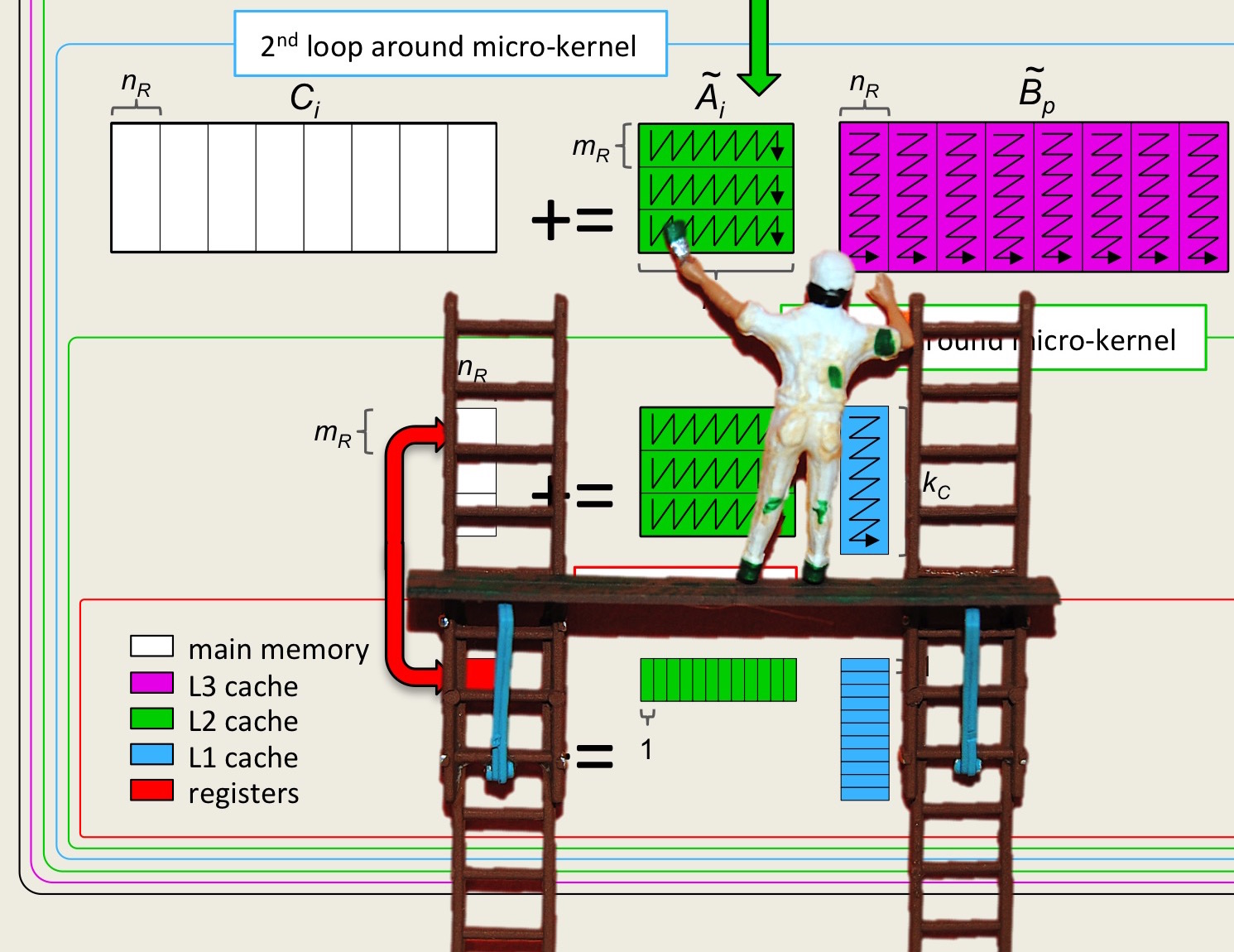
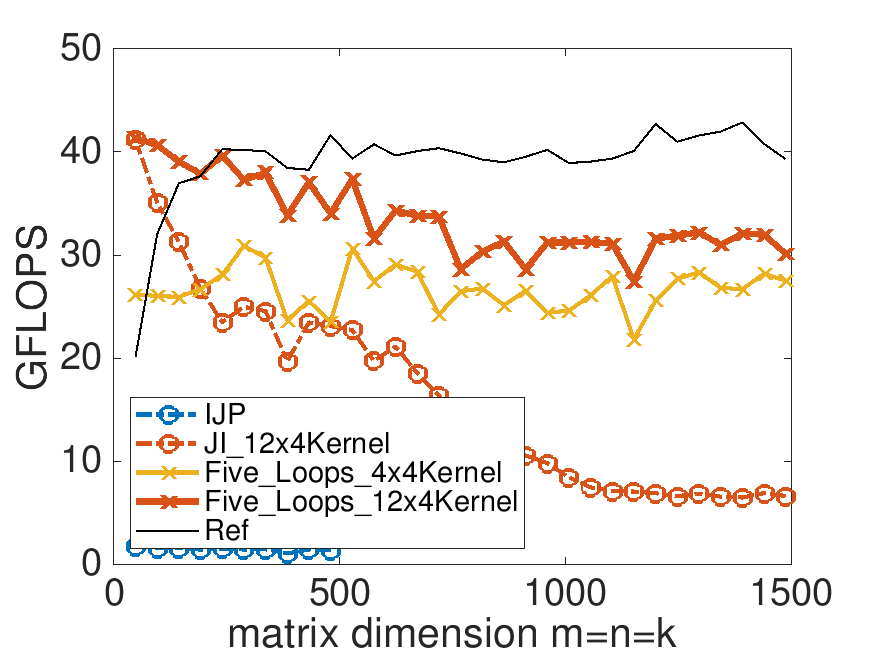
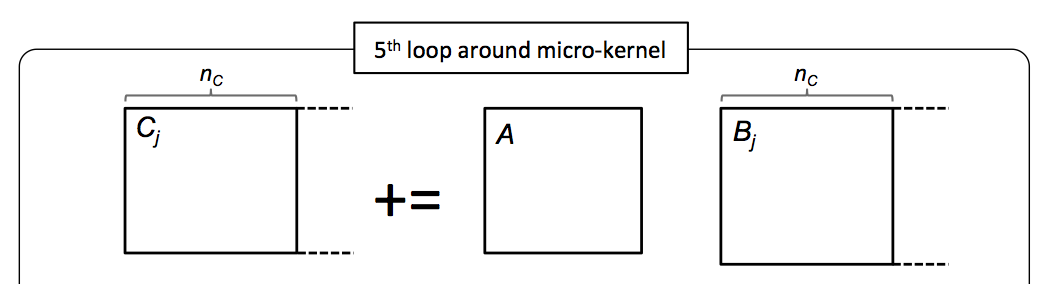
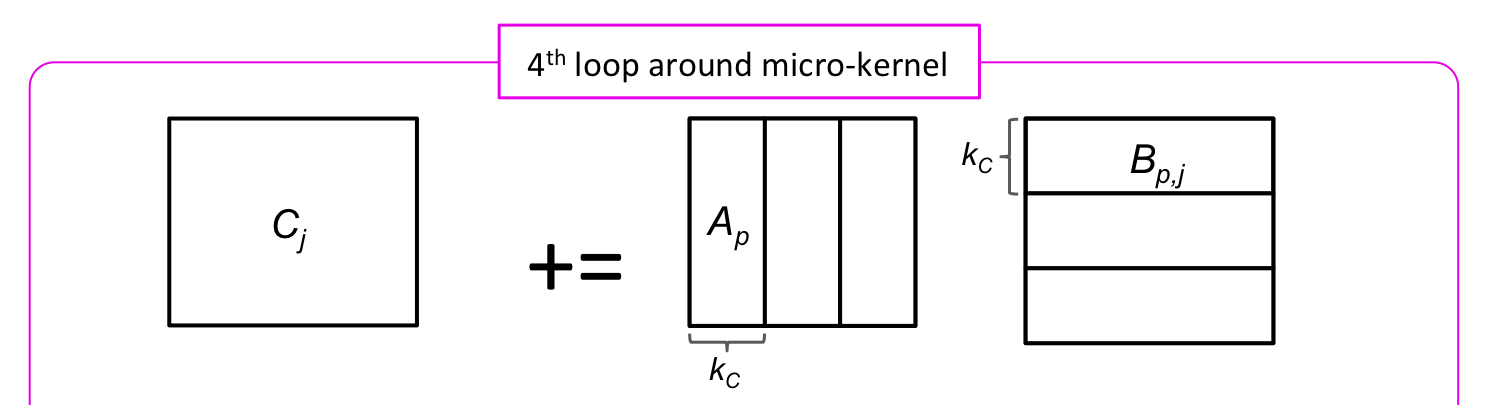
¶We always advocate, when it does not substantially impede performance, to instantiate an algorithm in code in a way that closely resembles how one explains it. In this spirit, the algorithm described in Figure 3.2.9 can be coded by making each loop (box) in the figure a separate routine. An outline of how this might be accomplished is illustrated next as well as in file Assignments/Week3/C/Gemm_Five_Loops_MRxNRKernel.c. You are asked to complete this code in the next homework.
void LoopFive( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int j=0; j<n; j+=NC ) {
int jb = min( NC, n-j ); /* Last loop may not involve a full block */
LoopFour( m, jb, k, A, ldA, &beta( , ), ldB, &gamma( , ), ldC );
}
}
void LoopFour( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int p=0; p<k; p+=KC ) {
int pb = min( KC, k-p ); /* Last loop may not involve a full block */
LoopThree( m, n, pb, &alpha( , ), ldA, &beta( , ), ldB, C, ldC );
}
}
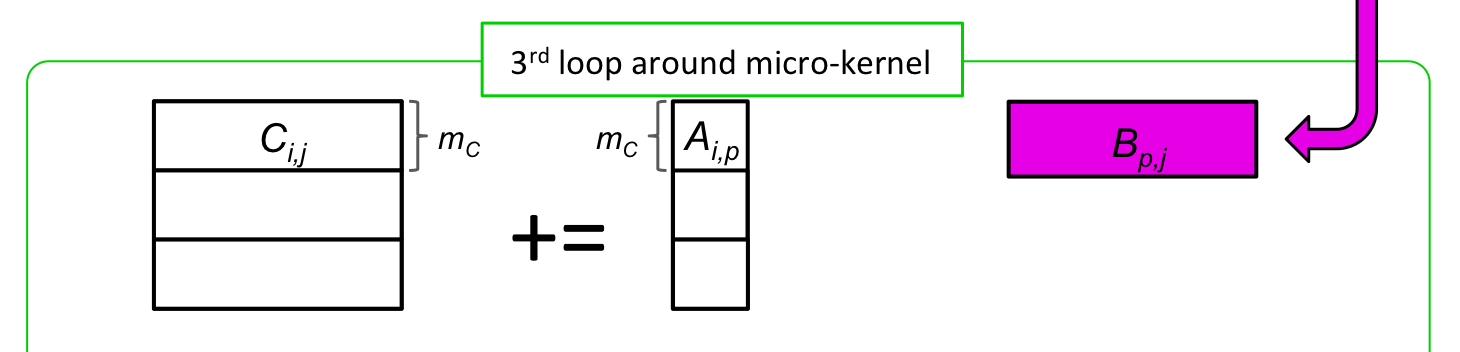
void LoopThree( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int i=0; i<m; i+=MC ) {
int ib = min( MC, m-i ); /* Last loop may not involve a full block */
LoopTwo( ib, n, k, &alpha( , ), ldA, B, ldB, &gamma( , ), ldC );
}
}
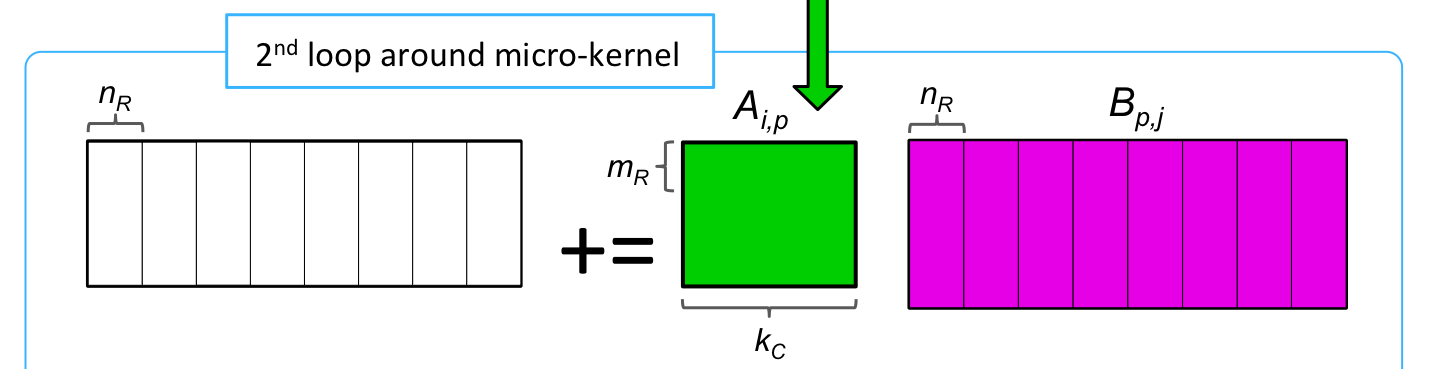
void LoopTwo( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int j=0; j<n; j+=NR ) {
int jb = min( NR, n-j );
LoopOne( m, jb, k, A, ldA, &beta( , ), ldB, &gamma( , ), ldC );
}
}
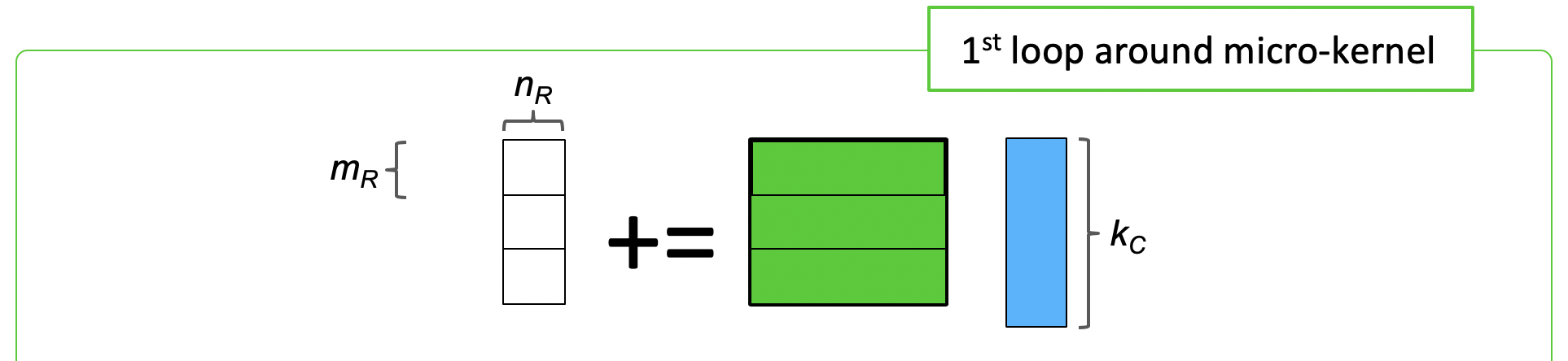
void LoopOne( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int i=0; i<m; i+=MR ) {
int ib = min( MR, m-i );
Gemm_MRxNRKernel( k, &alpha( , ), ldA, B, ldB, &gamma( , ), ldC );
}
}
Homework 3.2.6.1.
Complete the code in Assignments/Week3/C/Gemm_Five_Loops_MRxNRKernel.c and execute it with
make Five_Loops_4x4Kernel make Five_Loops_12x4KernelView the performance with Live Script
Assignments/Week3/C/data/Plot_Five_Loops.mlx.
Notice that these link the routines Gemm_4x4Kernel.c and Gemm_12x4Kernel.c that you completed in Homework 2.4.3.1 and Homework 2.4.4.4.
You may want to play with the different cache block sizes (MB, NB, and KB) in the Makefile. In particular, you may draw inspiration from Figure 3.2.8. Pick them to be multiples of \(12\) to keep things simple. However, we are still converging to a high-performance implementation, and it is still a bit premature to try to pick the optimal parameters (which will change as we optimize further).