Implementation of Matrix-Matrix Multiplication

 

Perhaps the best way to illustrate how the PLAPACK infrastructure can be used to code various parallel linear algebra algorithms is in detail discuss a reasonable simple example. For this we choose the parallel implementation of C = A B , where in our discussion we assume all three matrices are .

Algorithm

Computation of C = A B can be implemented by partitioning

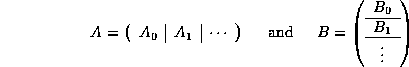
and noticing that

Thus the implementation of this operation can proceed as a sequence of rank-k updates [1, 5, 10].

Let us concentrate of one update: . Partitioning these matrices as they were when we discussed distribution of matrices yields

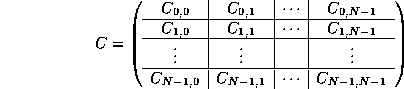
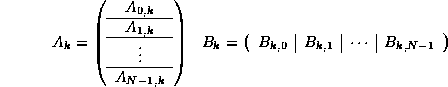
so that . Careful consideration shows that if the matrices are appropriately aligned, then duplicating within rows of nodes and within columns of nodes will allow local rank-k updates to proceed.

The more general case can be implemented using the following recursive algorithm:

scale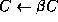
let and
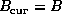
do until done: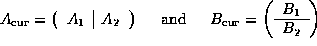

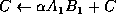
let and

PLAPACK implementation

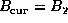
The PLAPACK implementation is given in CLICK HERE We explain the code line-by-line:

3-4 The matrices and constants are passed in linear algebra objects alpha, a, b, beta, and c.

8: Scale

14-16: Extract the datatype of the objects and create a multiscalar one that is duplicated to all nodes.

18-19: and .

20-22: Create duplicated projected multivectors to hold and after duplication within rows and columns, respectively.

24-28: Loop until the current matrices are empty.

28: Determine the width of and height of .

30-33:

35-37: Size the duplicated projected multivectors appropriately.

39-40: Indicate that and are oriented similar to multivectors projected onto a column and row of nodes, respectively.

42-43: Duplicate and . Notice that the input and output objects are described, after which all communication is hidden in this copy.

45: Perform updates to the local part of C , using the duplicated information.

46: Continue with and .

47-49: Cleanup of temporary objects.

Naturally, we are only trying to give a flavor of how such algorithms are implemented. For an example of a much more complex algorithm, the parallel implementation of reduction to banded form, see [11].

Performance

We discuss performance on three current generation distributed memory parallel computers: the Intel Paragon with GP nodes (one compute processor per node), the Cray T3D, and the IBM SP-2. In all cases we will report performance per node, where we use the term node for a compute processor. All performance is for 64-bit precision. The peak performance of an individual node limits the peak performance per node that can be achieved for our parallel implementations. The single processor peak performances for 64-bit arithmetic matrix-matrix multiply, using assembly coded sequential BLAS, are roughly given by 46 MFLOPS/sec for the Paragon, 120 MFLOPS/sec for the Cray T3D, and 210 MFLOPS/sec for the IBM SP-2. The speed and topology of the interconnection network affects how fast peak performance can be approached. Since our infrastructure is far from optimized with regards to communication as of this writing, there is no real need to discuss network speeds other than that both the Intel Paragon and Cray T3D have very fast interconnection networks, while the IBM SP-2 has a noticeably slower network, relative to individual processor speeds.

In Figure  CLICK HERE we show the performance on 64 node configurations of the different architectures. In that figure, the performance of the panel-panel variant is reported, with the matrix dimensions chosen so that all three matrices are square. The algorithmic and distribution blocking sizes, and nb were taken to be equal to each other ( ), but on each architecture they equal the value that appears to give good performance: on the Paragon and on the T3D and SP-2 . The different curves approach the peak performance for the given architecture, eventually leveling off.