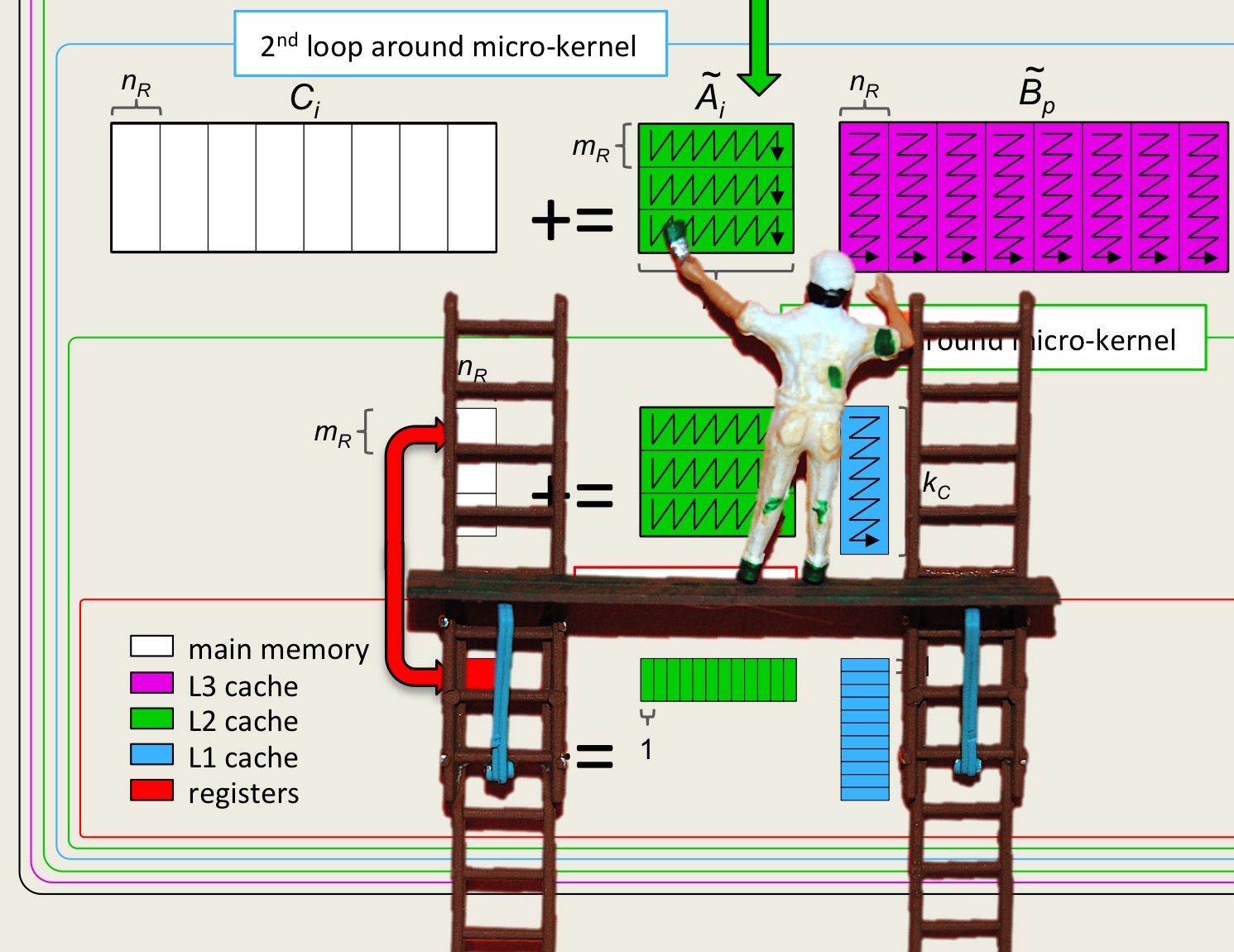
Unit 4.3.2 Parallelizing the first loop around the micro-kernel
¶Let us start by considering how to parallelize the first loop around the micro-kernel:

We then observed that the update of each row of \(C\) could proceed in parallel.
The matrix-matrix multiplication with the block of \(A\) and micro-panels of \(C\) and \(B \) performed by the first loop around the micro-kernel instead partitions the block of \(A \) into row (micro-)panels and the micro-panel of \(C\) into micro-tiles.
The bottom line: the updates of these micro-tiles can happen in parallel.
Homework 4.3.2.1.
In directory Assignments/Week4/C,
Copy Gemm_Five_Loops_Packed_MRxNRKernel.c into Gemm_MT_Loop1_MRxNRKernel.c.
Modify it so that the first loop around the micro-kernel is parallelized.
Execute it with
export OMP_NUM_THREADS=4 make MT_Loop1_8x6Kernel
Be sure to check if you got the right answer!
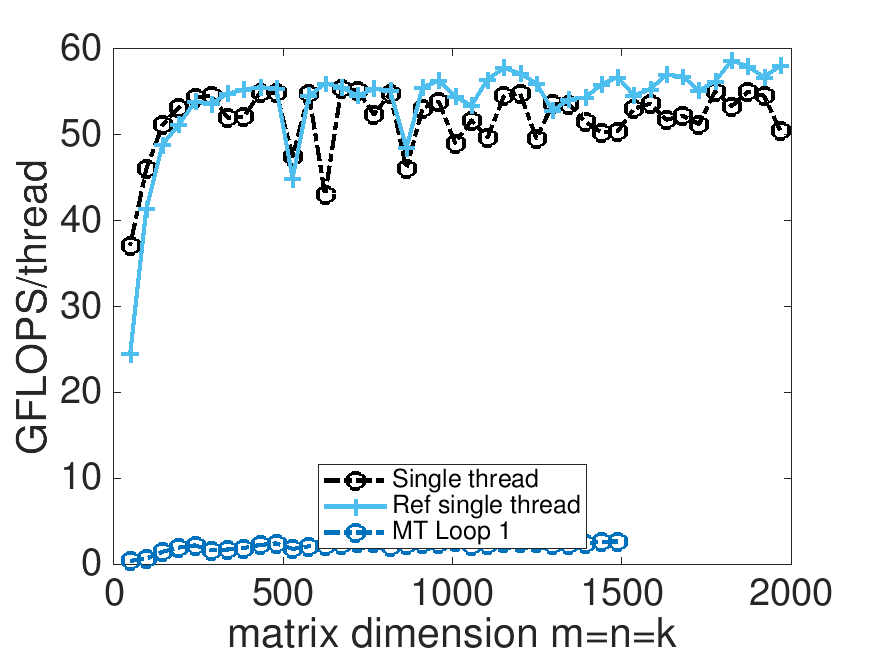
View the resulting performance with data/Plot_MT_performance_8x6.mlx, uncommenting the appropriate sections.
Parallelizing the first loop around the micro-kernel yields poor performance. A number of issues get in the way:
Each task (the execution of a micro-kernel) that is performed by a thread is relatively small and as a result the overhead of starting a parallel section (spawning threads and synchronizing upon their completion) is nontrivial.
-
In our experiments, we chose MC=72 and MR=8 and hence there are at most \(72/8=9\) iterations that can be performed by the threads. This leads to load imbalance unless the number of threads being used divides \(9\) evenly. It also means that no more than \(9 \) threads can be usefully employed. The bottom line: there is limited parallelism to be found in the loop.
This has a secondary effect: Each micro-panel of \(B\) is reused relatively few times by a thread, and hence the cost of bringing it into a core's L1 cache is not amortized well.
Each core only uses a few of the micro-panels of \(A \) and hence only a fraction of the core's L2 cache is used (if each core has its own L2 cache).
The bottom line: the first loop around the micro-kernel is not a good candidate for parallelization.