Remark 1.3.1
Since this course will discuss the computation \(C := A B + C \text{,}\) you will only need to remember the Greek letters \(\alpha \) (alpha), \(\beta \) (beta), and \(\gamma \) (gamma).
Linear algebra operations are fundamental to computational science. In the 1970s, when vector supercomputers reigned supreme, it was recognized that if applications and software libraries are written in terms of a standardized interface to routines that implement operations with vectors, and vendors of computers provide high-performance instantiations for that interface, then applications would attain portable high performance across different computer platforms. This observation yielded the original Basic Linear Algebra Subprograms (BLAS) interface [3] for Fortran 77, which are now referred to as the level-1 BLAS. The interface was expanded in the 1980s to encompass matrix-vector operations (level-2 BLAS)~\cite{BLAS2} and matrix-matrix operations (level-3 BLAS) [1].
An overview of the BLAS and how they are used to achieve portable high performance is given in the Encyclopedia of Parallel Computing [5]. This article is somewhat out of date. In a later enrichment we will point you to the BLAS-like Library Instantiation Software (BLIS) [6], which is now a widely used open source framework for rapidly instantiating the BLAS and similar functionality.
Expressing code in terms of the BLAS has another benefit: the call to the routine hides the loop that otherwise implements the vector-vector operation and clearly reveals the operation being performed, thus improving readability of the code.
In our discussions, we use capital letters for matrices (\(A, B, C, \ldots \)), lower case letters for vectors (\(a, b, c, \ldots \)), and lower case Greek letters for scalars (\(\alpha, \beta, \gamma, \ldots \)). Exceptions are integer scalars, for which we will use \(i, j, k, m, n,\) and \(p \text{.}\)
Vectors in our universe are column vectors or, equivalently, \(n \times 1 \) matrices if the vector has \(n \) components (size \(n \)). A row vector we view as a column vector that has been transposed. So, \(x \) is a column vector and \(x^T \) is a row vector.
In the subsequent discussion, we will want to expose the rows or columns of a matrix. If \(X \) is an \(m \times n\) matrix, then we expose its columns as
so that \(x_j \) equals the column with index \(j \text{.}\) We expose its rows as
so that \(\widetilde x_i^T \) equals the row with index \(i \text{.}\) Here the \(~^T\) indicates it is a row (a column vector that has been transposed). The tilde is added for clarity since \(x_i^T \) would in this setting equal the column indexed with \(i \) that has been transposed, rather than the row indexed with \(i \text{.}\) When there isn't a cause for confusion, we will sometimes leave the \(\widetilde ~\) off. We use the lower case letter that corresponds to the upper case letter used to denote the matrix, as an added visual clue that \(x_j \) is a column of \(X \) and \(\widetilde x_i^T \) is a row of \(X \text{.}\)
We have already seen that the scalars that constitute the elements of a matrix or vector are denoted with the lower Greek letter that corresponds to the letter used for the matrix of vector:
If you look carefully, you will notice the difference between \(x \) and \(\chi \text{.}\) The latter is the lower case Greek letter "chi."
Since this course will discuss the computation \(C := A B + C \text{,}\) you will only need to remember the Greek letters \(\alpha \) (alpha), \(\beta \) (beta), and \(\gamma \) (gamma).
Given two vectors \(x \) and \(y \) of size \(n \)
their dot product is given by
The notation \(x^T y \) comes from the fact that the dot product also equals the result of multiplying \(1 \times n\) matrix \(x^T \) times \(n \times 1 \) matrix \(y \text{.}\)
A routine. coded in C, that computes \(x^T y + \gamma \) where \(x \) and \(y \) are stored at location x with stride incx and location y with stride incy, respectively, and \(\gamma \) is stored at location gamma is given by
#define chi( i ) x[ (i)*incx ] // map chi( i ) to array x
#define psi( i ) y[ (i)*incy ] // map psi( i ) to array y
void Dots( int n, double *x, int incx, double *y, int incy, double *gamma )
{
for ( int i=0; i<n; i++ )
*gamma += chi( i ) * psi( i );
}
in Assignments/Week1/C/Dots.c. Here stride refers to the number of items in memory between the stored components of the vector. For example, the stride when accessing a row of a matrix is lda when the matrix is stored in column-major order with leading dimension lda.
The BLAS include a function for computing the dot operation. Its calling sequence in Fortran, for double precision data, is
DDOT( N, X, INCX, Y, INCY )where
(input) N is an integer that equals the size of the vectors.
(input) X is the address where \(x \) is stored.
(input) INCX is the stride in memory between entries of \(x \text{.}\)
(input) Y is the address where \(y \) is stored.
(input) INCYnnnn is the stride in memory between entries of \(y \text{.}\)
The function returns the result as a scalar of type double precision. If the datatype were single precision, complex double precision, or complex single precision, then the first D is replaced by S, Z, or C, respectively.
To call the same routine in a code written in C, it is important to keep in mind that Fortran passes data by address. The call
Dots( n, x, incx, y, incy, &gamma );which, recall, adds the result of the dot product to the value in gamma, translates to
gamma += ddot_( &n, x, &incx, y, &incy );When one of the strides equals one, as in
Dots( n, x, 1, y, incy, &gamma );one has to declare an integer variable (e.g, i_one) with value one and pass the address of that variable:
int i_one=1; gamma += ddot_( &n, x, &i_one, y, &incy );We will see examples of this later in this section.
In this course, we use the BLIS implementation of the BLAS as our library. This library also has its own (native) BLAS-like interface that we refer to as the BLIS Typed API. (BLIS is actually a framework for the rapid instantiation of BLAS-like functionality. It comes with four different interfaces to that functionality: The classic Fortran BLAS interface, the CBLAS interface for the C language (which is an interface that is rarely used), the BLIS Typed API with is reminiscent of the BLAS interface, but with added functionality and flexibility, and the BLIS object API, which which a Users' Guide can be found at https://github.com/flame/blis/blob/master/docs/BLISObjectAPI.md.) A Users' Guide for this interface can be found at https://github.com/flame/blis/blob/master/docs/BLISTypedAPI.md. There, we find the routine bli_ddotxv that computes \(\gamma := \alpha x^T y + \beta \gamma \text{,}\) optionally conjugating the elements of the vectors. The call
Dots( n, x, incx, y, incy, &gamma );translates to
double one=1.0;
bli_ddotxv( BLIS_NO_CONJUGATE, BLIS_NO_CONJUGATE,
n, &one, x, incx, y, incy, &one, &gamma );
The BLIS_NO_CONJUGATE is to indicate that the vectors are not to be conjugated. Those parameters are there for consistency with the complex versions of this routine (bli_zdotxv and bli_cdotxv).Let us return once again to the IJP ordering of the loops that compute matrix-matrix multiplication:
This pseudo-code translates into the routine coded in C given in Figure 1.1.1.
Unit 1.3.2\(C \)\(A \)\(B \)We then notice that
If this makes your head spin, you will want to quickly go through Weeks 3-5 of our MOOC titled "Linear Algebra: Foundations to Fontiers,.'' which is an introductory undergraduate course. It captures that the outer two loops visit all of the elements in \(C \text{,}\) and the inner loop implements the dot product of the appropriate row of \(A \) with the appropriate column of \(B \text{:}\) \(\gamma_{i,j} := \widetilde a_i^T b_j + \gamma_{i,j} \text{,}\) as illustrated by
which is, again, the IJP ordering of the loops.
In directory Assignments/Week1/C copy file Assignments/Week1/C/Gemm_IJP.c into file Gemm_IJ_Dots.c. Replace the inner-most loop with an appropriate call to Dots, and compile and execute them with
make IJ_Dots
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_P.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_P_m.mlx.
In directory Assignments/Week1/C copy file Assignments/Week1/C/Gemm_IJ_Dots.c into file Gemm_IJ_ddot.c. Replace the call to Dots to a call to the BLAS routine ddot, and compile and execute them with
make IJ_ddot
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_P.mlx (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_P_m.mlx.)
In directory Assignments/Week1/C copy file Assignments/Week1/C/Gemm_IJ_Dots.c into file Gemm_IJ_ddotxv.c. Replace the call to Dots to a call to the BLIS routine bli_bli_ddotxv, and compile and execute them with
make IJ_bli_ddotxv
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_P.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_P_m.mlx.)
Obviously, one can equally well switch the order of the outer two loops, which just means that the elements of \(C \) are computed a column at a time rather than a row at a time:
Repeat the last exercises with the implementation in Assignments/Week1/C/Gemm_JIP.c. In other words, copy this file into files Gemm_JI_Dots.c, Gemm_JI_ddot.c, and Gemm_JI_bli_ddotxv.c. Make the necessary changes to these file, and compile and execute them with
make JI_Dots make JI_ddot make JI_bli_ddotxv
View the resulting performance with the Live Script in Assignments/Week1/C/data/Plot_Inner_P.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_P_m.mlx.)
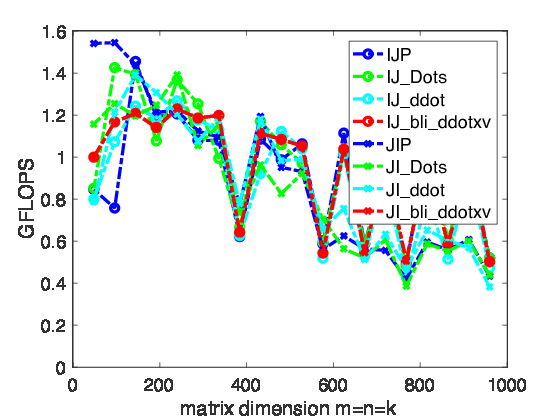
In Figure~\ref{fig:IJP_JIP} we report the performance of the various implementations from the last homeworks. What we notice is that, at least when using Apple's clang compiler, not much difference results from hiding the inner-most loop in a subroutine.
Given a scalar, \(\alpha \text{,}\) and two vectors, \(x \) and \(y \text{,}\) of size \(n \) with elements
which in terms of the elements of the vectors equals
The name axpy comes from the fact that in Fortran 77 only six characters and numbers could be used to designate the names of variables and functions. The operation \(\alpha x + y \) can be read out loud as "scalar apha times x plus y" which yields the acronym axpy.
An outline for a routine that implements the axpy operation is given by
#define chi( i ) x[ (i)*incx ] // map chi( i ) to array x
#define psi( i ) y[ (i)*incy ] // map psi( i ) to array y
void Axpy( int n, double alpha, double *x, int incx, double *y, int incy )
{
for ( int i=0; i<n; i++ )
psi(i) +=
}
in file Assignments/Week1/C/Axpy.c.
Complete the routine in LAFF-On-HPC/Assignments/C/Week1/C/Axpy.c. You will test the implementation by using it in subsequent homeworks.
The BLAS include a function for computing the axpy operation. Its calling sequence in Fortran, for double precision data, is
DAXPY( N, ALPHA, X, INCX, Y, INCY )
where
(input) N is the address of the integer that equals the size of the vectors.
(input) ALPHA is the address where \(\alpha \) is stored.
(input) X is the address where \(x \) is stored.
(input) INCX is the address where the stride between entries of \(x \) is stored.
(input/output) Y is the address where \(y \) is stored.
(input) INCY is the address where the stride between entries of \(y \) is stored.
It may appear strange that the addresses of N, ALPHA, INCX, and INCY are passed in. This is because Fortran passes parameters by address rather than value.) If the datatype were single precision, complex double precision, or complex single precision, then the first D is replaced by S, Z, or C, respectively.
In C, the call
Axpy( n, alpha, x, incx, y, incy );
translates to
daxpy_( &n, &alpha, x, &incx, y, &incy );
which links to the Fortran interface. Notice that the scalar parameters n, alpha, incx, and incy are passed "by address" because Fortran passes parameters to subroutines by address. We will see examples of its use later in this section.
The BLIS native routine for axpy is bli_dapyv. The call
Axpy( n, alpha, x, incx, y, incy );translates to
bli_daxpyv( BLIS_NO_CONJUGATE, n, alpha, x, incx, y, incy );
The BLIS_NO_CONJUGATE is to indicate that vector \(x \) is not to be conjugated. That parameter is there for consistency with the complex versions of this routine (bli_zaxpyv and bli_caxpyv).
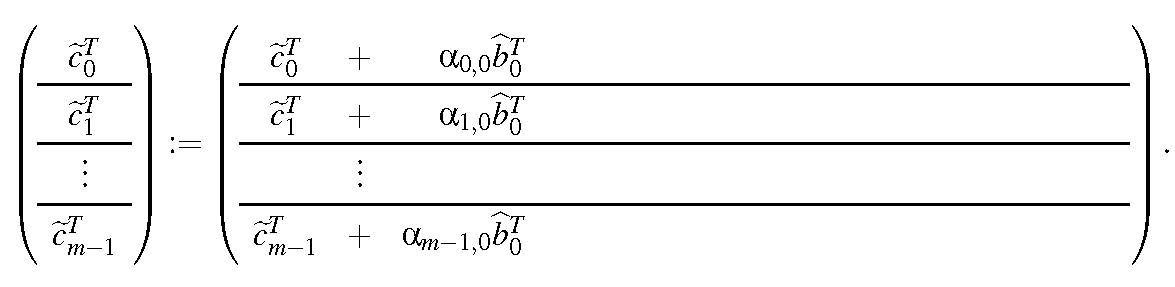
In an implementation of the algorithm for computing \(C := A B + C \) given by
and illustrated by
one can now replace the loop indexed by \(j \) with a call to Axpy.
Complete the following routine
#define alpha( i,j ) A[ (j)*ldA + i ] // map alpha( i,j ) to array A
#define beta( i,j ) B[ (j)*ldB + i ] // map beta( i,j ) to array B
#define gamma( i,j ) C[ (j)*ldC + i ] // map gamma( i,j ) to array C
void Axpy( int, double, double *, int, double *, int );
void MyGemm( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int i=0; i<m; i++ )
for ( int p=0; p<k; p++ )
Axpy( n, alpha( i,p ), &beta( p,0 ), ldB, &gamma( i,0 ), ldC );
}
You can find the partial implementation in Assignments/Week1/C/Gemm_IP_Axpy.c test the implementation with Live Script TestGemm_IP_Axpy.mlx.
What we notice is that there are \(3! \) ways of order the loops: Three choices for the outer loop, two for the second loop, and one choice for the final loop. Let's consider the IPJ ordering:
One way to think of the above algorithm is to view matrix \(C \) as its rows, matrix \(A \) as its individual elements, and matrix \(B\) as its rows:
We then notice that
This captures that the outer two loops visit all of the elements in \(A \text{,}\) and the inner loop implements the updating of the \(i \)th row of \(C \) by adding \(\alpha_{i,p} \) times the \(p \)th row of \(B \) to it, as captured by
In directory Assignments/Week1/C copy file Assignments/Week1/ into file Gemm_IP_Axpy.c. Replace the inner-most loop with a call to Axpy, and compile and execute them with
make IP_Axpy
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_J.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_J_m.mlx.)
In directory Assignments/Week1/C copy file Assignments/Week1/ into file Gemm_IP_daxpy.c. Replace the inner-most loop with a call to the BLAS routine daxpy, and compile and execute them with
make IP_daxpy
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_J.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_J_m.mlx.)
In directory Assignments/Week1/C copy file Assignments/Week1/ into file Gemm_IP_bli_daxpyv.c, and compile and execute with
make IP_bli_daxpyv
Replace the inner-most loop with a call to the BLIS routine bli_daxpyv. View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_J.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_J_m.mlx.)
One can switch the order of the outer two loops to get
The outer loop in this second algorithm fixes the row of \(B\) that is used to to update all rows of \(C \text{,}\) using the appropriate element from \(A \) to scale. In the first iteration of the outer loop (\(p = 0 \)), the following computations occur:

Repeat the last exercises with the implementation in Assignments/Week1/C/Gemm_PIJ.c. In other words, copy this file into files Gemm_PI_Axpy.c, Gemm_PI_daxpy.c, and Gemm_PI_bli_daxpyv.c. Make the necessary changes to these files, and compile and execute them with
make PI_Axpy make PI_daxpy make PI_bli_daxpyv
View the resulting performance with the Live Script in Assignments/Week1/C/data/Plot_Inner_J.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_J_m.mlx.)
Let us consider the JPI ordering:
Another way to think of the above algorithm is to view matrix \(C \) as its columns, matrix \(A \) as its columns, and matrix \(B \) as its individual elements. Then
so that
The algorithm captures this as
In directory Assignments/Week1/C copy file Assignments/Week1/C/Gemm_JPI.c into file Gemm_JP_Axpy.c. Replace the inner-most loop with a call to Axpy, and compile and execute with
make JP_Axpy
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_I.mlxdata/Plot_Inner_I.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_I_m.mlx.)
In directory Assignments/Week1/C copy file Assignments/Week1/C/Gemm_JPI.c into file Gemm_JP_daxpy.c. Replace the inner-most loop with a call to the BLAS routine daxpy, and compile and execute with
make JP_daxpy
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_I.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_I_m.mlx.)
In directory Assignments/Week1/C copy file Assignments/Week1/C/Gemm_JPI.c into file Gemm_JP_bli_daxpyv.c. Replace the inner-most loop with a call to the BLIS routine bli_daxpyv, and compile and execute with
make JP_bli_daxpyv
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_I.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_I_m.mlx.)
One can switch the order of the outer two loops to get
The outer loop in this algorithm fixes the column of \(A \) that is used to to update all columns of \(C \text{,}\) using the appropriate element from \(B \) to scale. In the first iteration of the outer loop, the following computations occur:

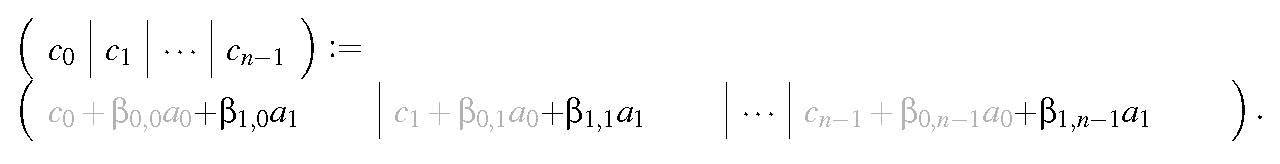
Repeat the last exercises with the implementation in Assignments/Week1/C/Gemm_PJI.c. In other words, copy this file into files Gemm_PJ_Axpy.c, Gemm_PJ_daxpy.c, and Gemm_PJ_bli_daxpyv.c. Then, make the necessary changes to these files, and compile and execute with
make PJ_Axpy make PJ_daxpy make PJ_bli_daxpyv
View the resulting performance by making the necessary changes to the Live Script in Assignments/Week1/C/data/Plot_Inner_I.mlx. (Alternatively, use the script in Assignments/Week1/C/data/Plot_Inner_I_m.mlx.)
The purpose of this section was mostly to help you think in terms of operations with vectors (the rows and columns of the matrices) when reasoning about, and implementing, the inner-most loop of the different algorithms for computing a matrix-matrix multiplication. On Robert's laptop, the performance is not much affected. For this reason, in the below exercise, we revisit the performance graphs for the different loop orderings from Section~\ref{sec:AllOrderings}.

In Figure 1.3.3, the results of Homework 1.2.5 on Robert's laptop are again reported. What do the two loop orderings that result in the best performances have in common? You may want to use the following worksheet to answer this question:
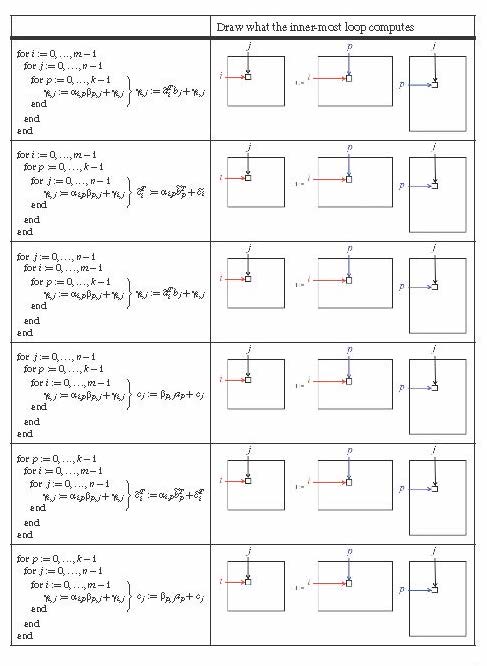
They both have the loop indexed with \(i \) as the inner-most loop and that loop computes with columns of \(C \) and \(A \text{.}\)
In Homework 1.3.15, why do they get better performance?
Matrices are stored with column major order, accessing contiguous data usually yields better performance, and data in columns are stored contiguously.
In Homework 1.3.15, why does the implementation that gets the best performance outperform the one that gets the next to best performance?
The JPI loop ordering accesses columns of C and A in the inner loop. The column of C is read and written while the column of A is only read. The column of C is read and written while the column of A is only read. The JPI loop ordering keeps the column of C in cache memory which reduced the number of times it is read from and written to main memory.
One thing that is obvious from all the exercises so far is that the gcc compiler doesn't do a very good job of automatically reordering loops to improve performance, at least not for the way we are writing the code.