In his recent paper, “Faster Coherent Quantum Algorithms for Faster Phase, Energy, and Amplitude Estimation”, UTCS PhD graduate Patrick Rall puts forth novel quantum algorithms for estimating important fundamental qualities of our complex world. Patrick’s approach simplifies the necessary computations compared to the current standard method. Estimation of these properties has applications in condensed matter physics and quantum chemistry as well as machine learning and finance. 

In quantum mechanics, the task of measuring observed qualities like energy, charge, and conductivity can be a complicated task due to quantum randomness. When looking at the world through a mathematical lens, everything you observe is encoded into a big and complicated matrix, and the actual value is the solution to an equation involving this matrix. Fortunately, quantum computers are very good at solving this equation. 

However, there is a key restriction on the type of matrix that is easy to solve this way. Patrick’s research hones in on the requirement for a matrix to be unitary. The matrix used to generate energy values, the Hamiltonian, is famously non-unitary and complicates this calculation. Without a new algorithm to simplify this scenario, scientists were forced to use traditional methods. These methods are cumbersome due to the fact that the Hamiltonian simulates the passage of time (which is unitary) from which then energy is found through the extra step of Fourier analysis.  Patrick broke free of this restriction and utilized block encoding to, according to him, “let quantum computers talk about whatever matrices we want by working with the Hamiltonian directly.”

So, how can quantum computers manipulate non-unitary matrices? Basically, the computer translates the matrix that wasn't originally unitary into a larger unitary matrix. This is the overarching logic that we bring to the specific non-unitary matrix we are trying to solve: the Hamiltonian. Patrick leverages a standard method developed by Andrew Childs, Robin Kothari, and their co-authors that constructs a unitary matrix with the Hamiltonian in the top left corner.

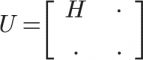
Once we have loaded the Hamiltonian onto the quantum computer, we have all the information we need to find the energy. This is the job of Patrick’s method. First, the algorithm writes the energy as a series of bits (0s and 1s) using a binary expansion. Then, for each bit, it applies a polynomial to the Hamiltonian that calculates that bit as a function of the energy (see figure). The result is an observable that indicates just that bit of the energy. Finally, it measures the observable for each bit, and puts them back together into a numerical value for the energy.

This is represented by this figure: 

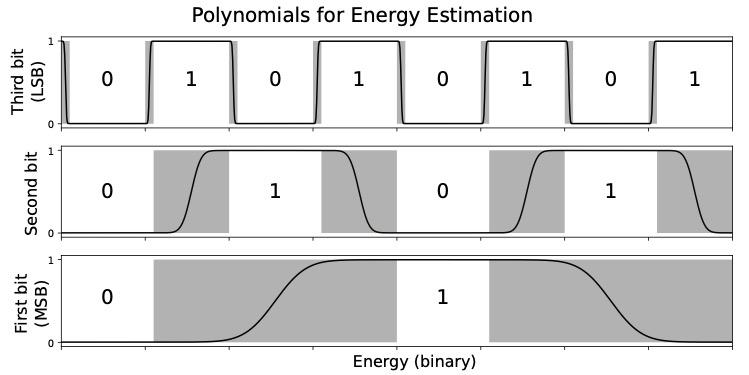
Each horizontal layer represents the value of a bit in the binary expansion of the energy. The horizontal layer at the bottom of the graph represents the Most Significant Bit (MSB) and the highest layer represents the Least Significant Bit (LSB). The polynomials that indicate the bits need to jump up and down at different speeds.

This provides a way to estimate energies expressed by the Hamiltonian in a way that is about 20 times more efficient than previous methods.